The Table Method: How to approach high school word problems in a unified and systematic way
It was a math lesson like countless before. It was early March, and the entrance exam for the prestigious Swiss upper high schools was approaching fast. I had been preparing my students, 'in-betweeners' who had not passed the first time, extensively. Ten math lessons per week, non-stop exam preparation, since August. We had covered the whole curriculum and were reviewing selected topics.
This particular day was dedicated to word problems. We were discussing a standard, run-of-the-mill time-distance problem:
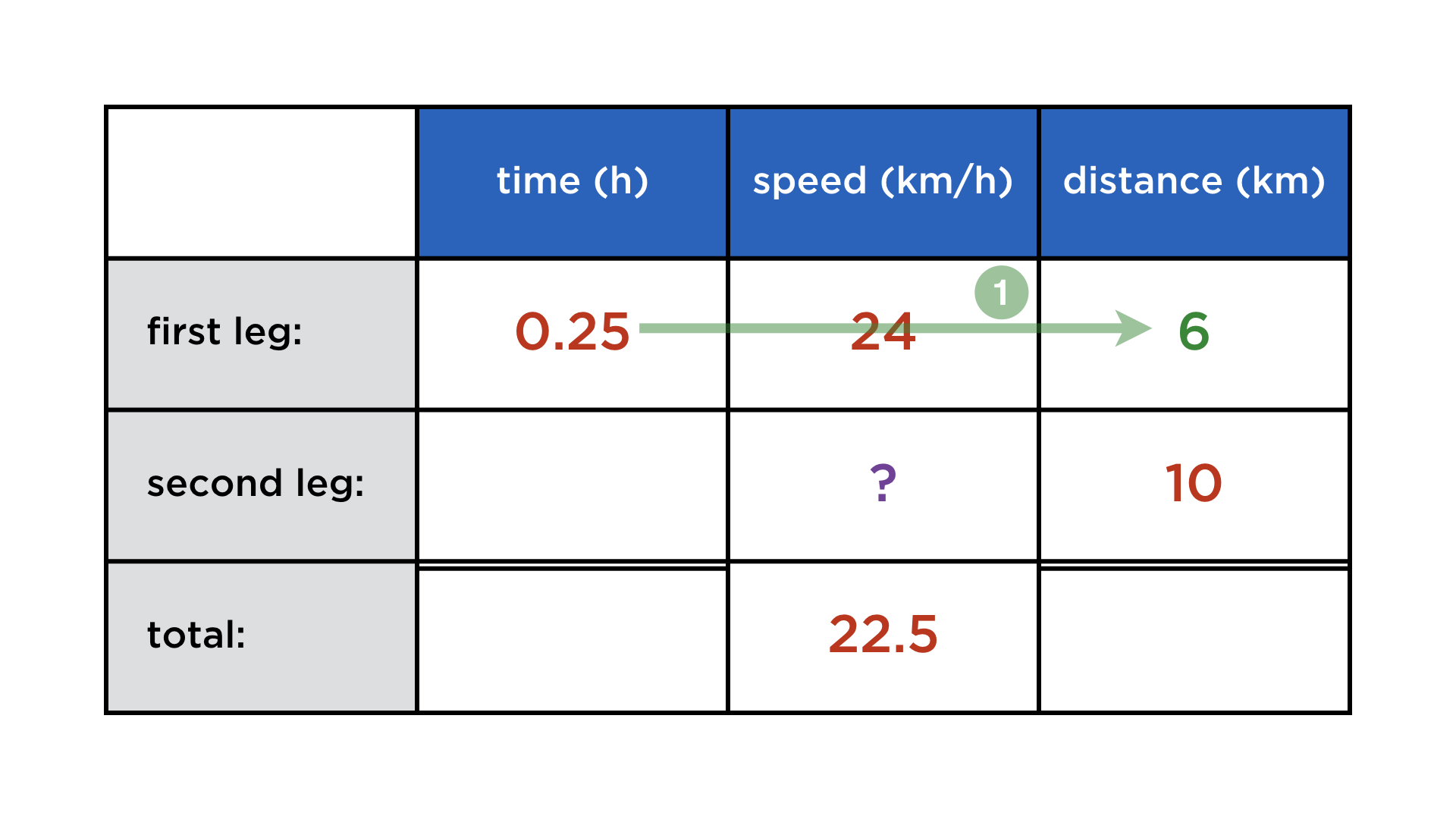
A cyclist takes 15 min to complete the first leg of a trip, if she cycles at a speed of 24 km/h. Find out how fast she has to travel on the second leg, measuring 10 km, so that her average speed over the whole distance is 22.5 km/h.
There are more exciting problems to wonder about in mathematics, but that is a topic (read: rant) for another day. In class, we went through the usual steps:
- the first leg ist 0.25 h x 24 km/h = 6 km long
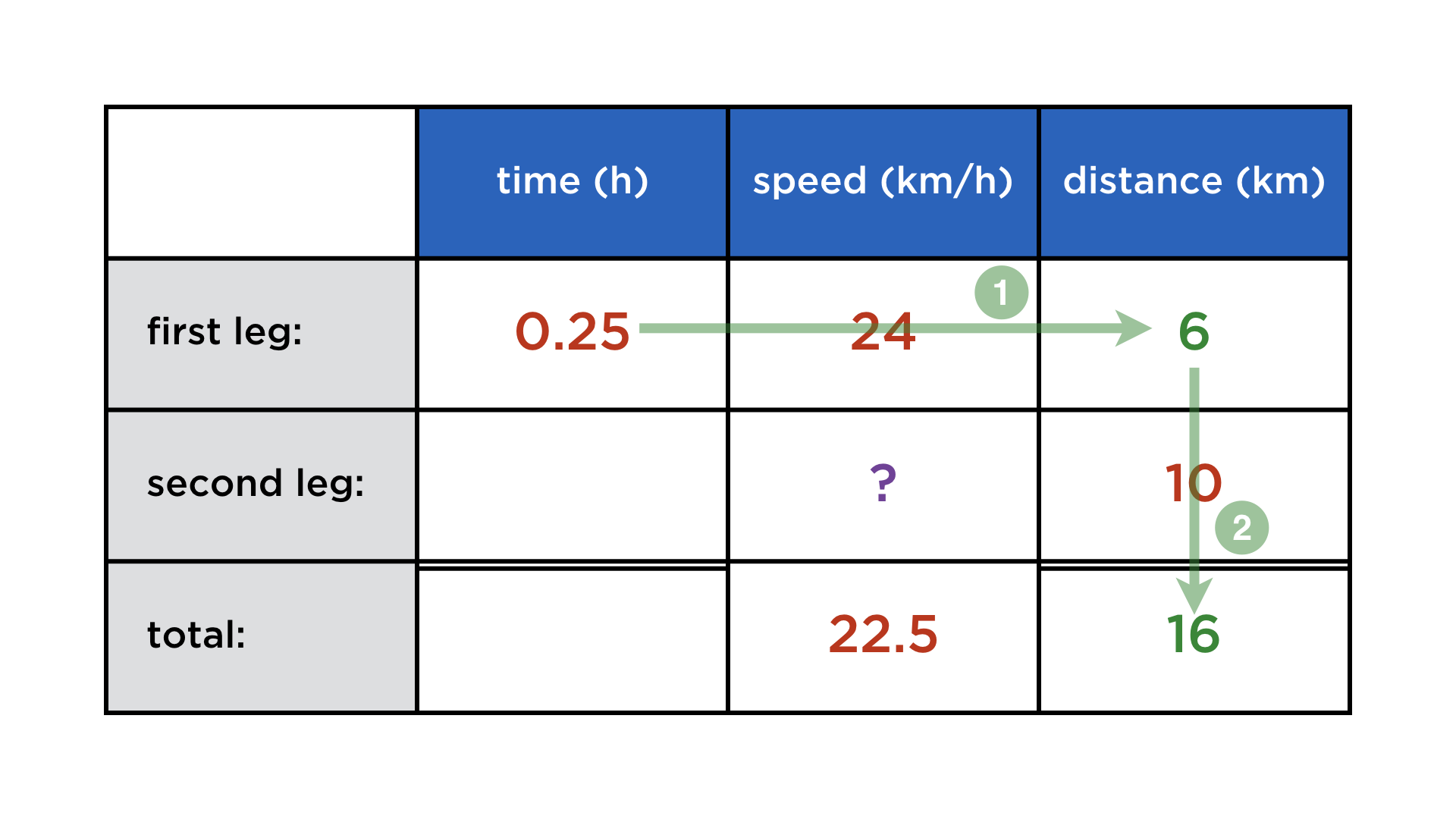
- the total distance is therefore 6 km + 10 km = 16 km
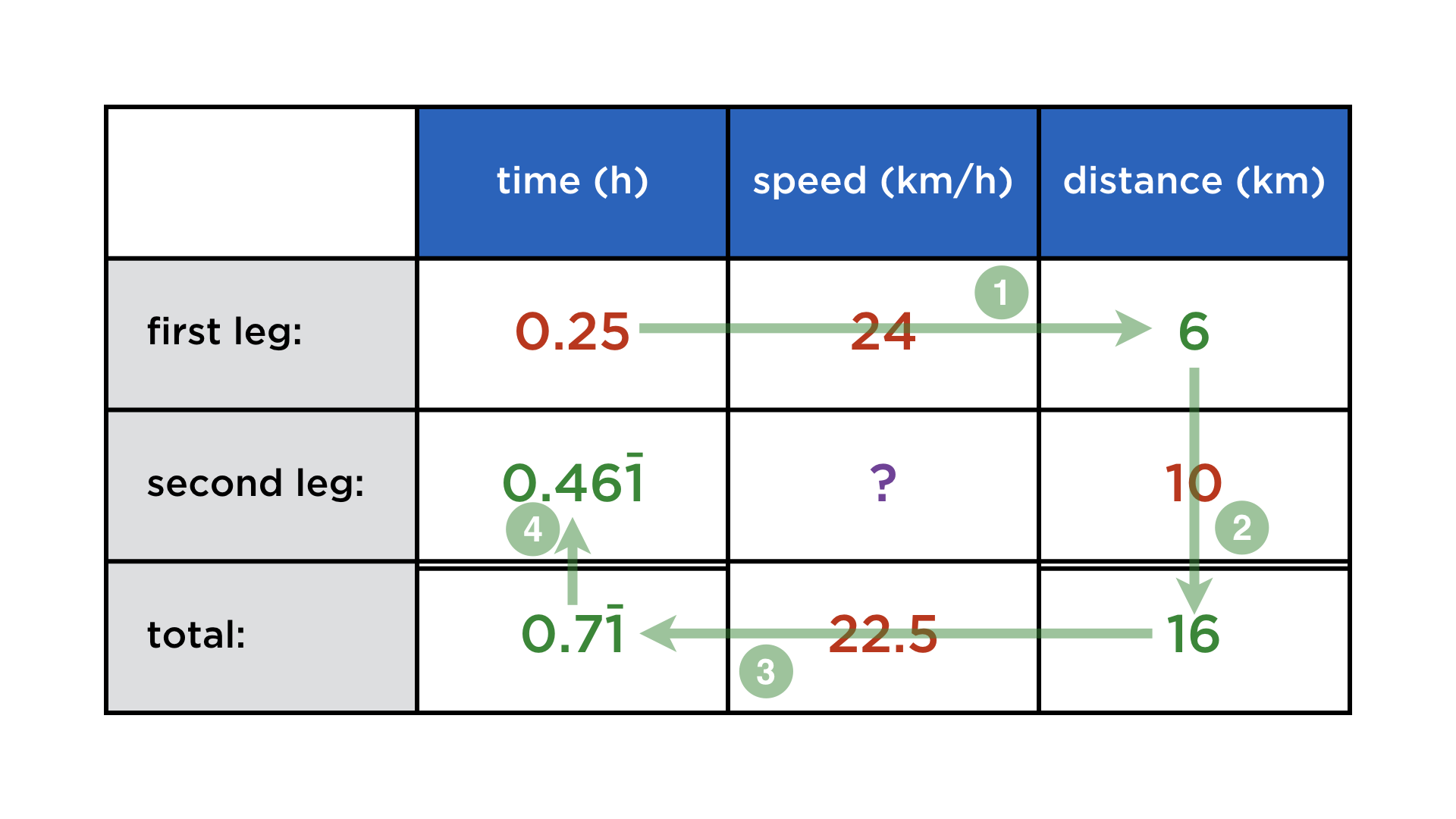
- the total travel time is 16 km / 22.5 km/h = 0.71 h ( = 42 min 40 s)
- the travel time on the second leg is therefore 0.71 h – 0.25 h = 0.461 h ( = 27 min 40 s)
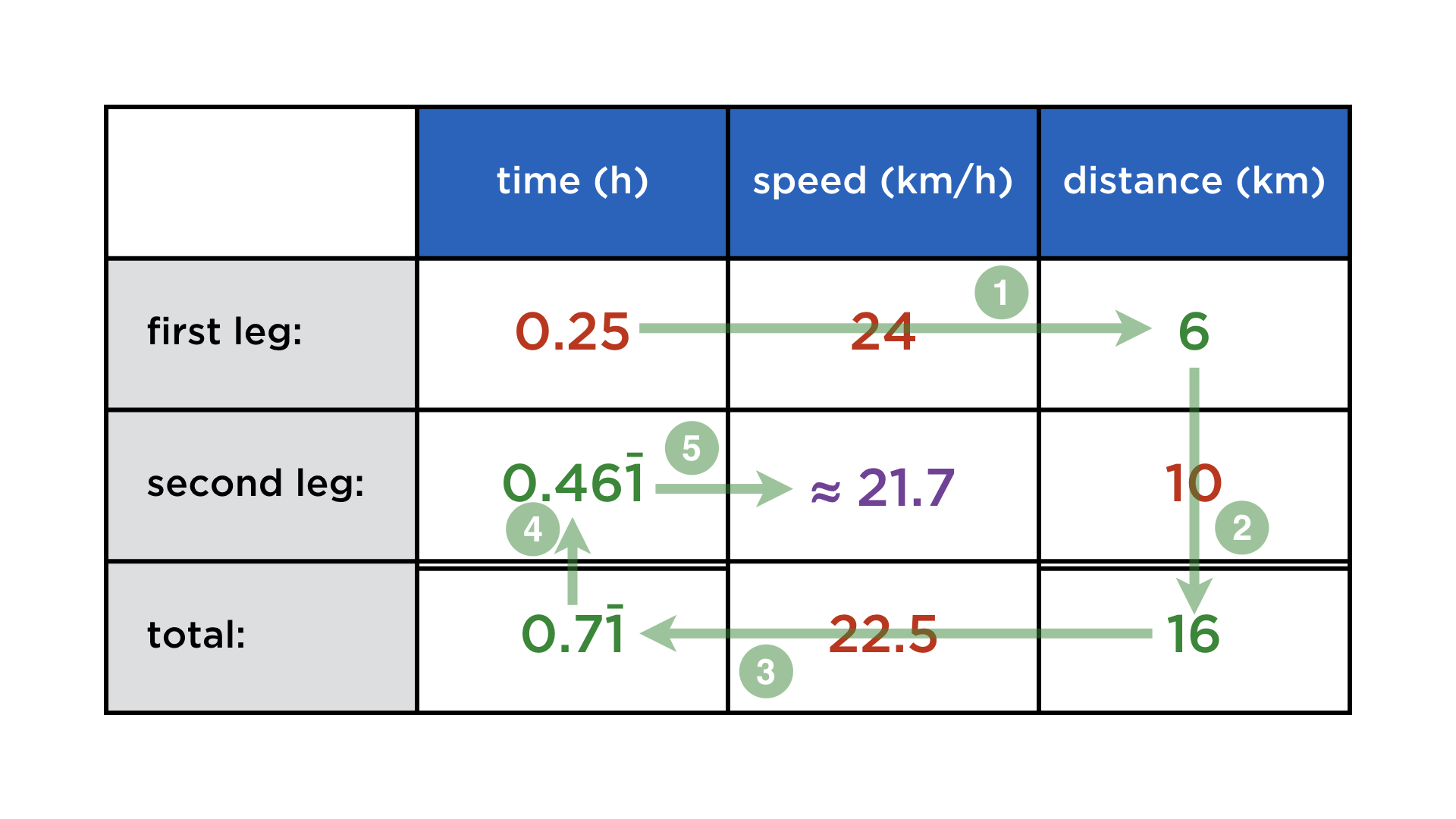
- the speed over the the second leg is thus 10 km / 0.461 h ≈ 21.7 km/h
Did I say we went through these steps? My bad, I meant I. My students could follow each one of them, but were at a complete loss on how to find them in the first place. It seemed like black magic, but then again: "Mr. Hambrecht, when you explain it, it's obvious!"
How often had I been with a class at that exact same spot? I've lost count.
WHY ARE WORD PROBLEMS SO HARD?
One of the main difficulties with word problems is the inability to recognize where to start. The above problem contains four given quantities, and requires five steps to solve. This is far beyond the one- or two-step problems from elementary school. Students can feel overwhelmed by the sheer number of possible combinations of given numbers and operations. Of course, most of those combinations make no sense, but that is exactly what separates the trained eye from the apprentice. How is a novice in chess supposed to choose from the 20 possible first moves? Or solve a chess problem? Even if they can follow other player's explanations on why a particular move is good, and another bad, they will often be hard-pressed to come up with their own.
I bring up this analogy because word problems, much like chess, lack a unifying system for finding such solutions. Checking a given solution, on the other hand, is much easier. Patterns for finding good moves in chess exist, but they are so manifold that it still takes the proverbial 10 000 hours to learn them. When we try to teach pattern recognition in word problems, we encounter the same problem: the patterns are apparently so few and far between that each new problem effectively appears unique.
But this is not so. There exist deep, unifying and beautiful analogies between the plethora of seemingly unrelated word problems. They share common algebraic structures whose representations can please the aesthetic sensibility in any mathematician's mind. The following examples will show what I mean.
CYCLING BACK
Let's go back to that fateful math lesson. We were all looking puzzled at the worked solution on the blackboard. The students wondering how to get to such a solution on their own, me wondering how to get that skill from my head into theirs.
But then something happened. Out of the blue, perhaps just to summarize, I drew a table:
There are three triplets of the relationship "time x speed = distance", one for each leg and one for the whole trip: those are the rows. And of course, the times and distances add up (but not the speeds): those are the columns. With these links in mind, the steps for completing the table fell into place (click on the arrows to show them):
"It's just like a sudoku!" exclaimed one of the students.
For the first time, a time-distance problem seemed tractable to them. Graphing the problem helps to visualize it, but gives no immediate clues on how to actually compute an answer. In a table, the known and unknown quantities are ordered along their algebraic relationships, immediately suggesting each next step.
We all learned something that day. I made a mental note of exploring this method for other kinds of problems. Over the following days and lessons, it dawned on me just how powerful it was.
GIMME SUGAR
The word problems in the entrance exams seemed to be tailored for precisely this method: a lot of them e. g. invariably contained some sort of weighted average, without calling it such. Here is another example:
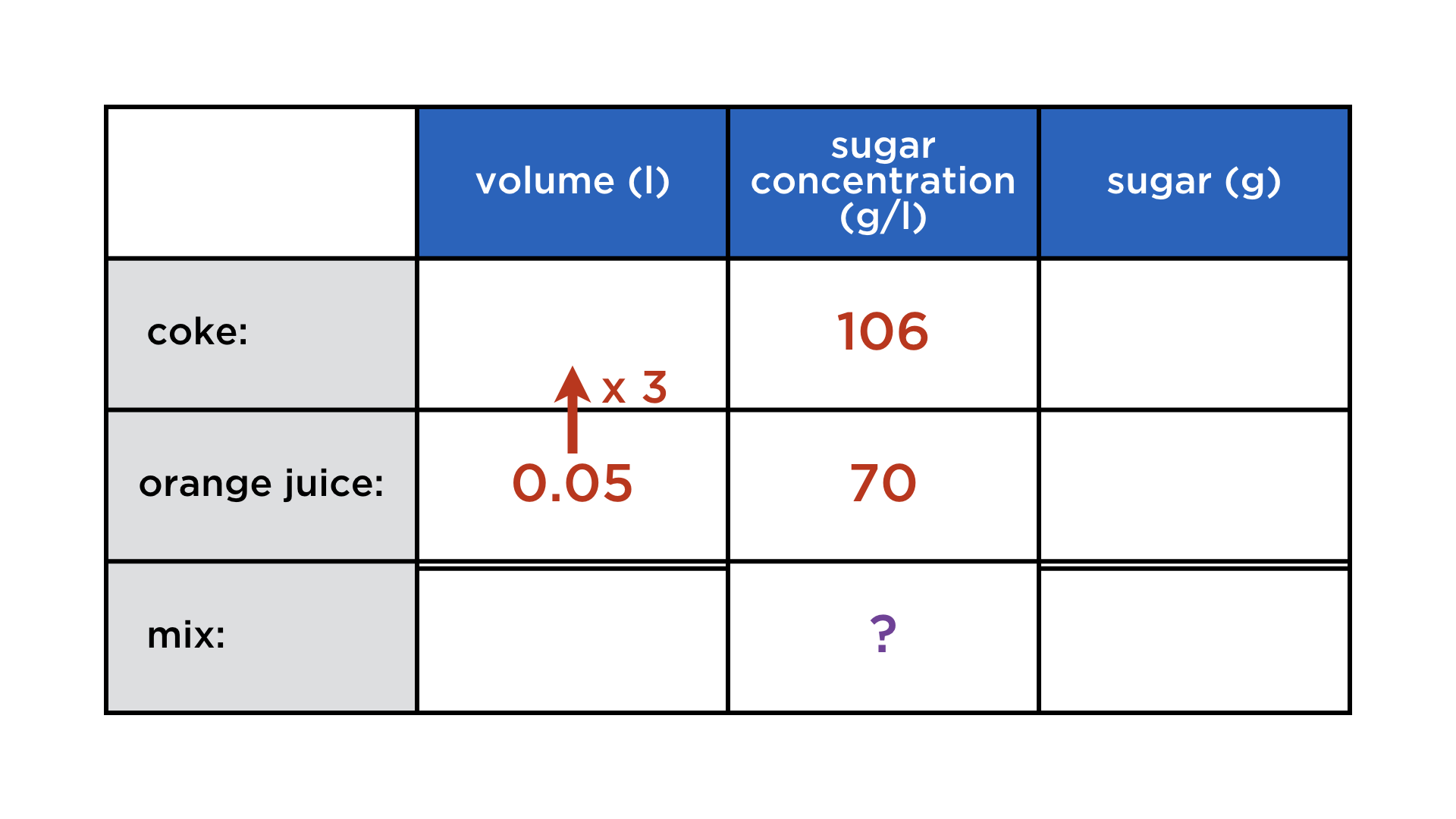
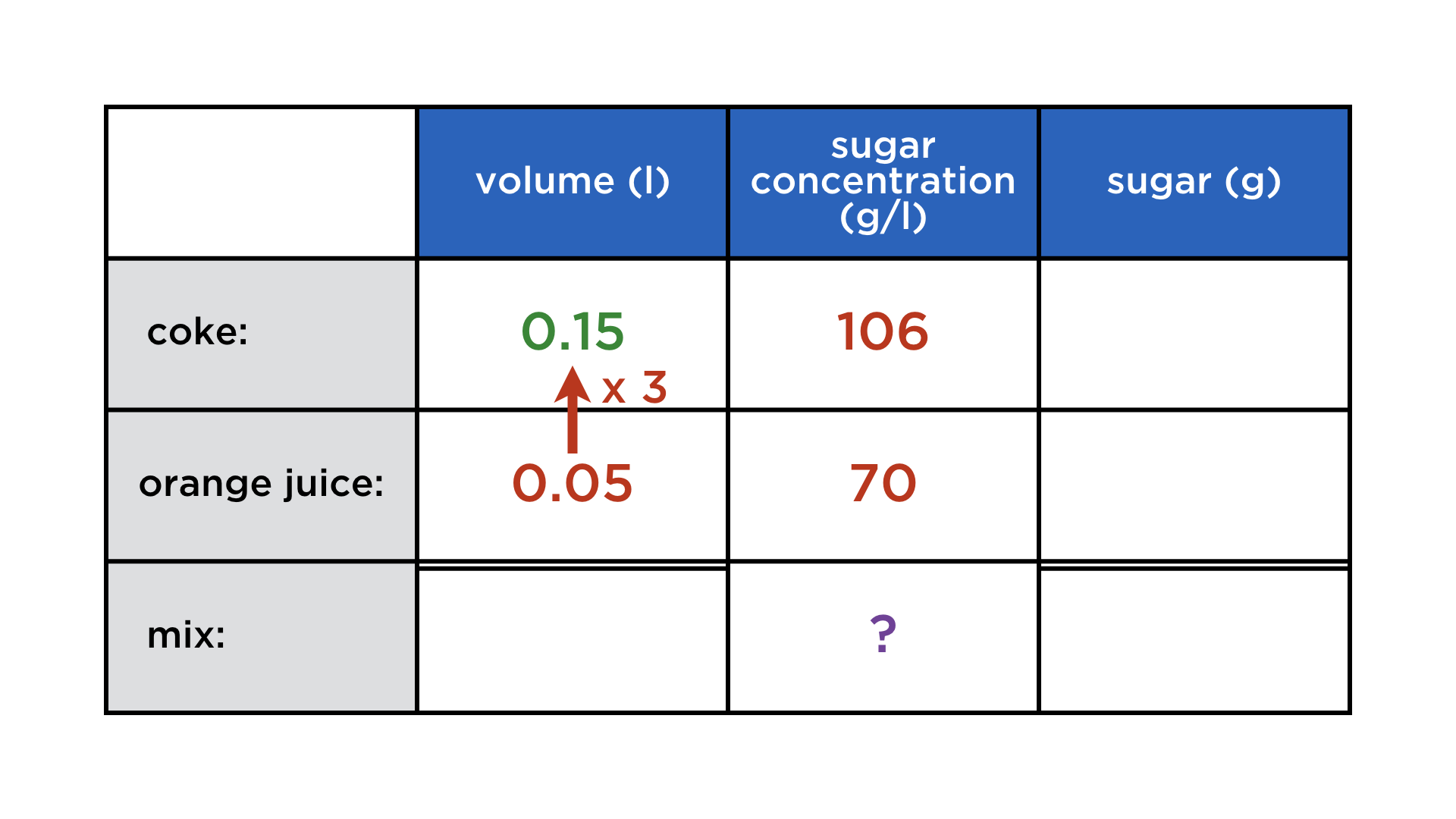
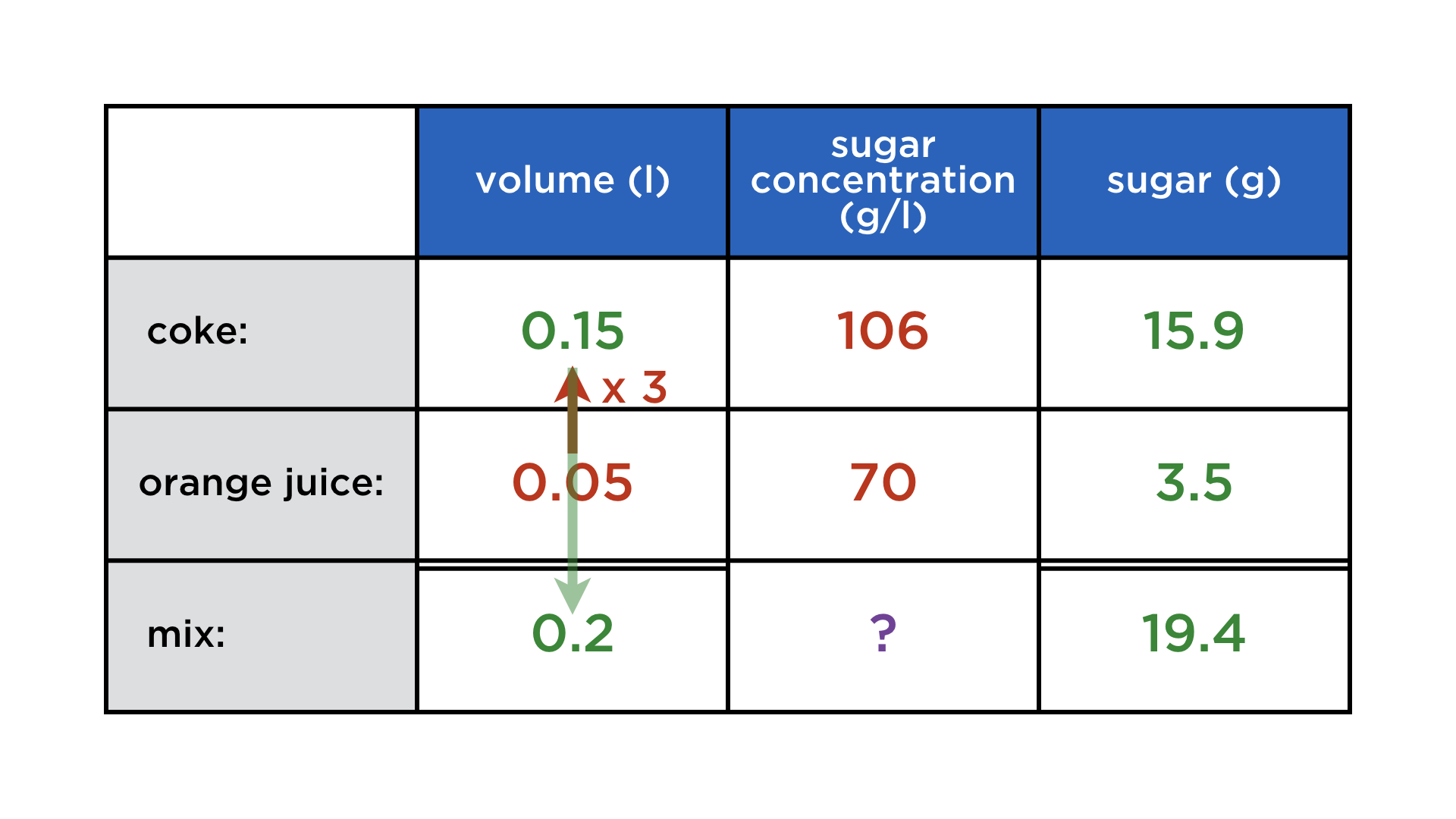
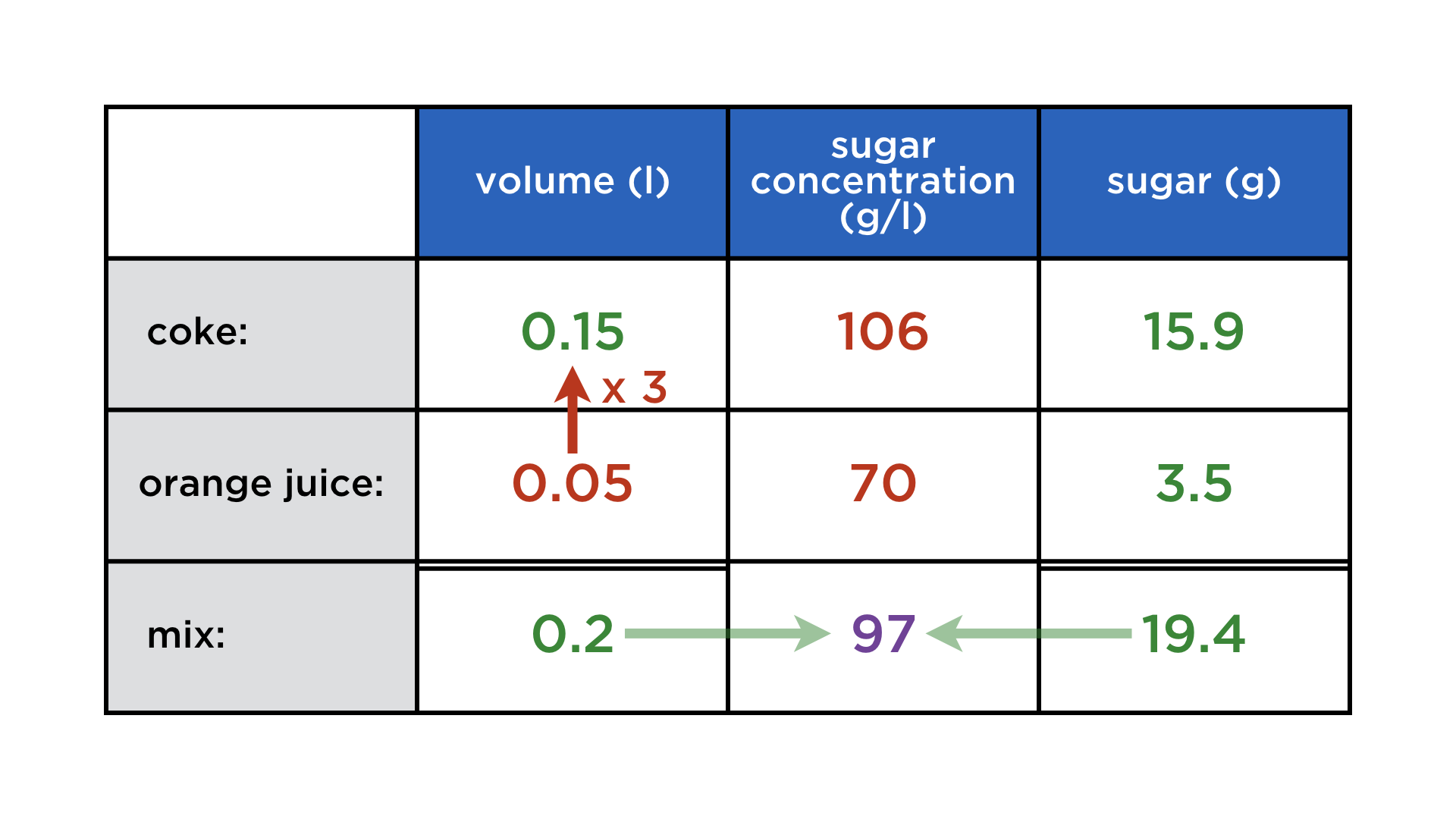
Carl likes to mix coke with orange juice, to make it less sweet. Coke has a sugar concentration of 106 g/l, while orange juice contains 70 g of sugar per liter. Now Carl is mixing 50 ml of orange juice with a threefold quantity of coke. What is the sugar concentration (in g/l) of the mix?
Three columns, linked by multiplication:
volume (l) x sugar concentration (g/l) = sugar content (g).
Three rows: pure coke, pure orange juice, and the mix. Again, volumes and sugar contents add up, but not the concentrations:
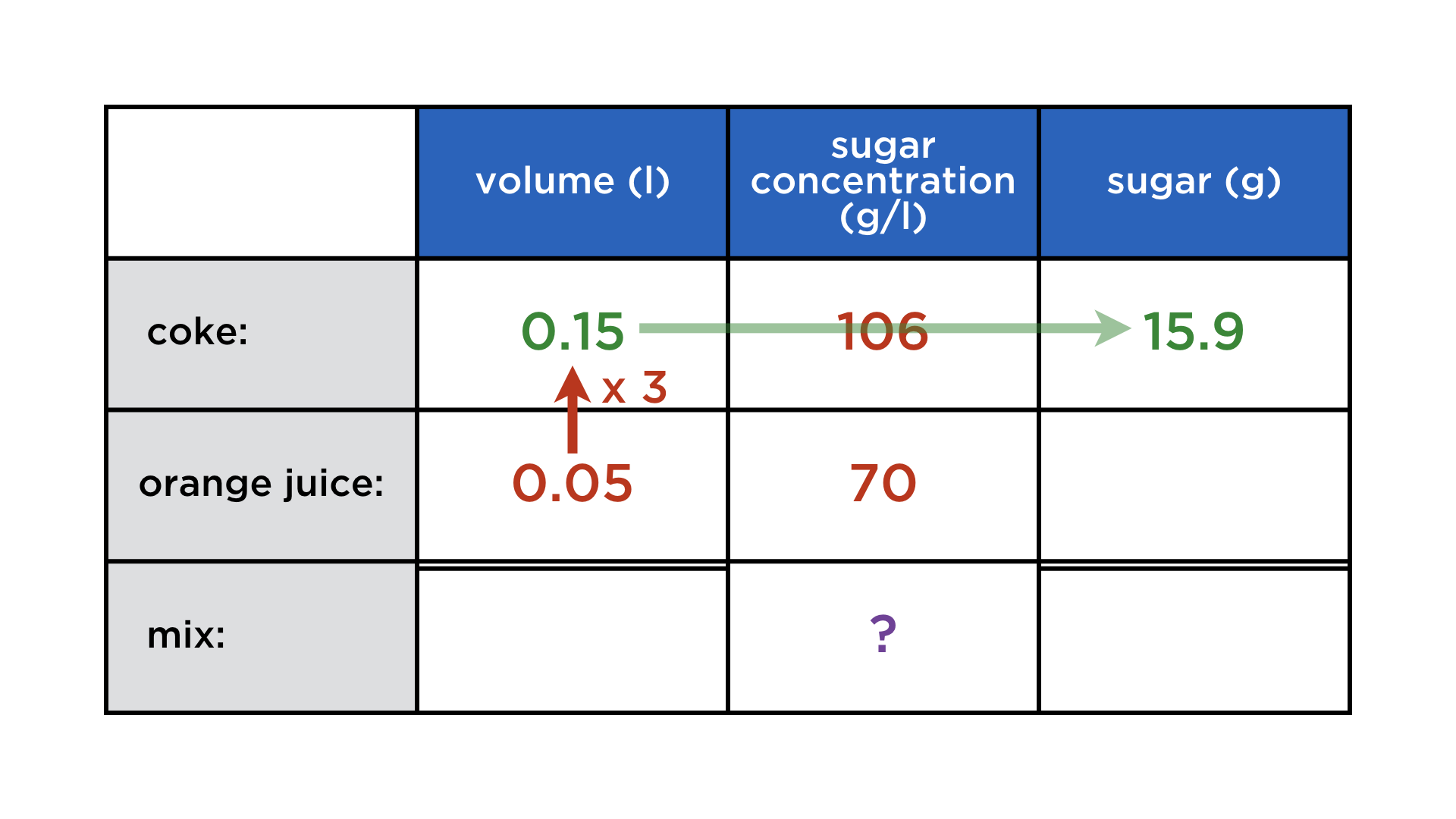
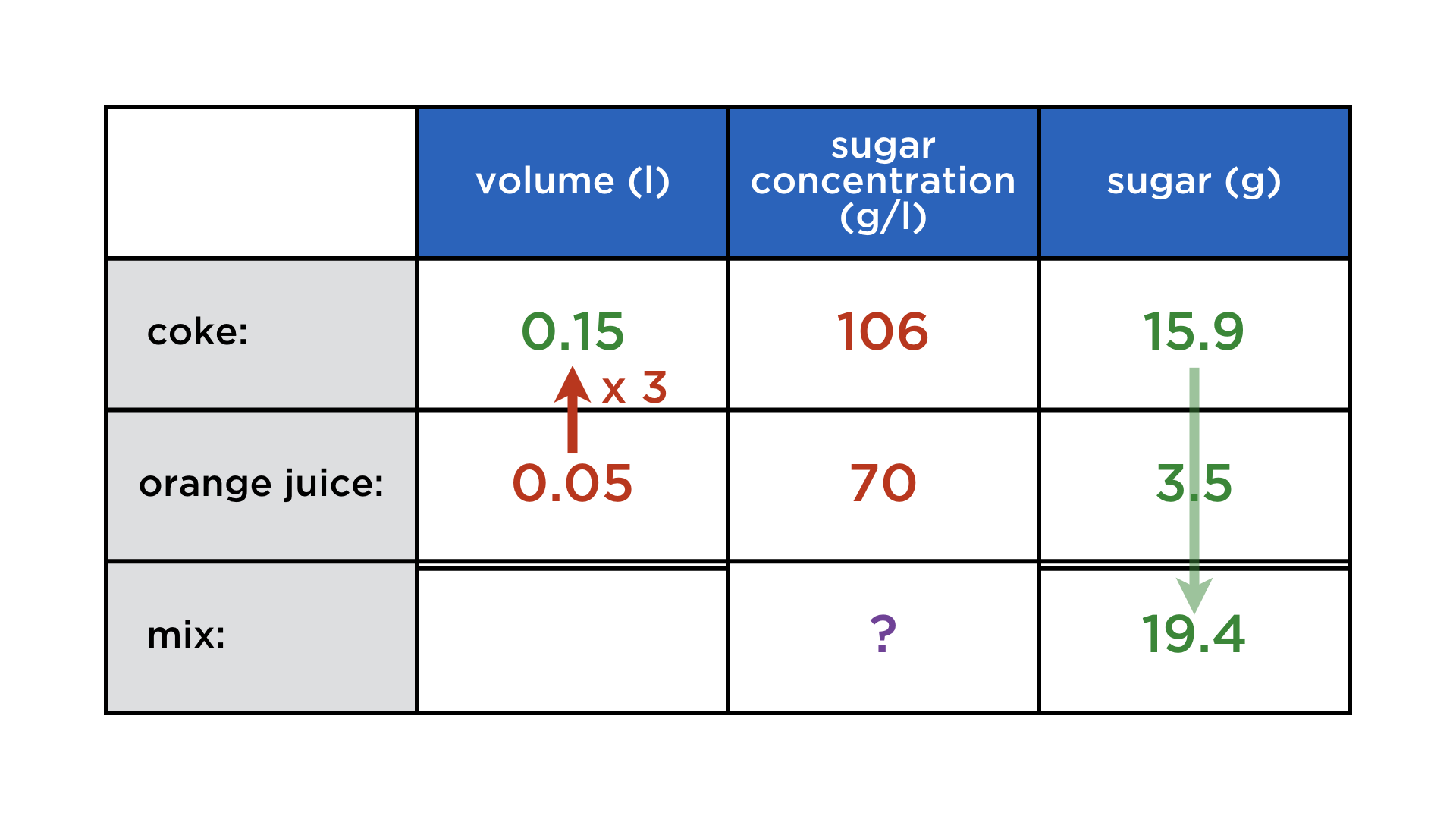
The red arrow represents the datum "three times more coke than orange juice". We get to the concentration by first finding everything else:
The algebraic structure of this problem is exactly the same as in the previous time-distance problem. Instead of an average speed, we have an average concentration (which becomes realized once the coke and juice mix). Only the distribution of known and unknown quantities has changed.
CECI N'EST PAS UNE PIPE
But the really funny thing is that tables can also be used to solve other, apparently unrelated kinds of word problems:
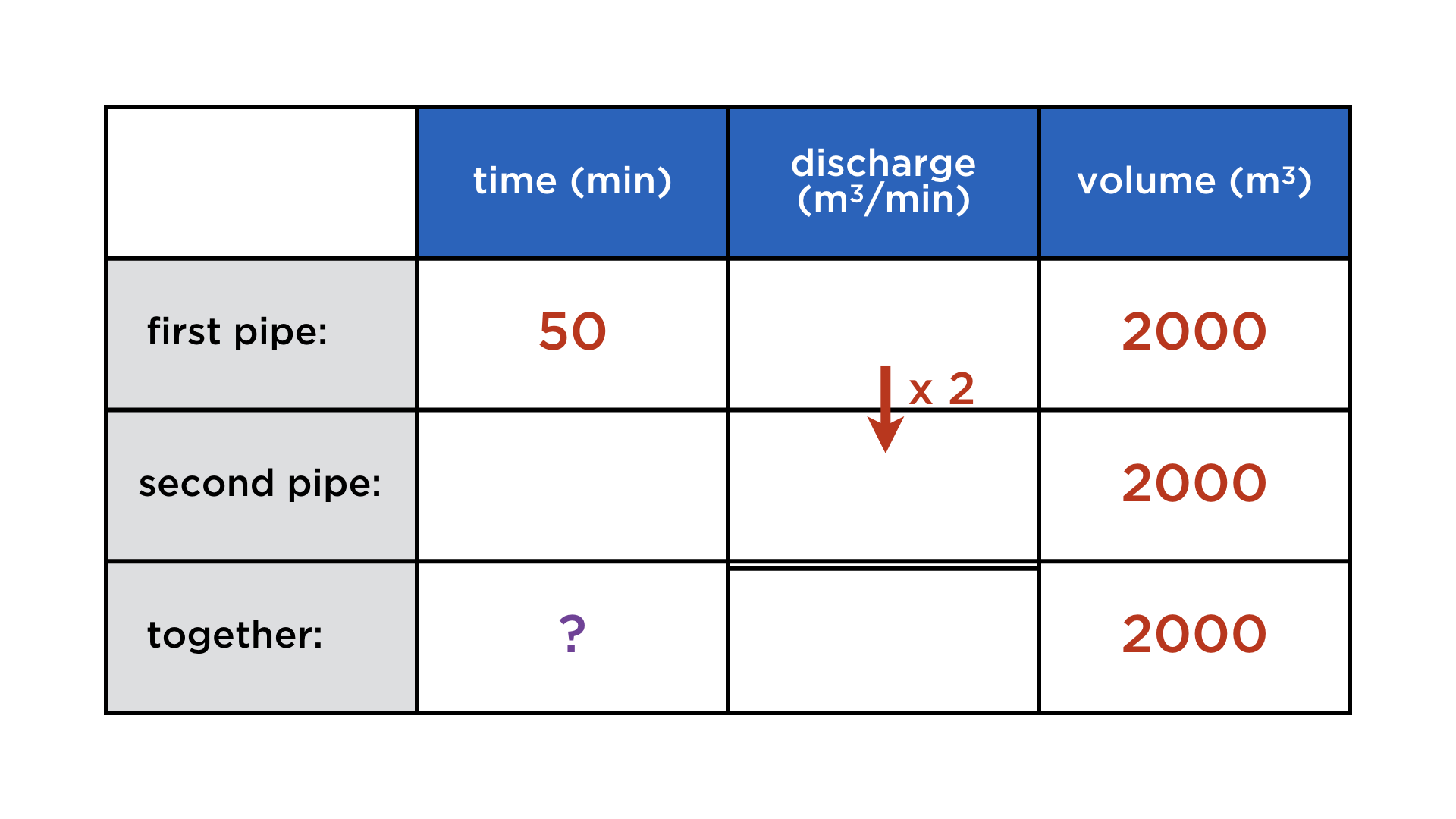
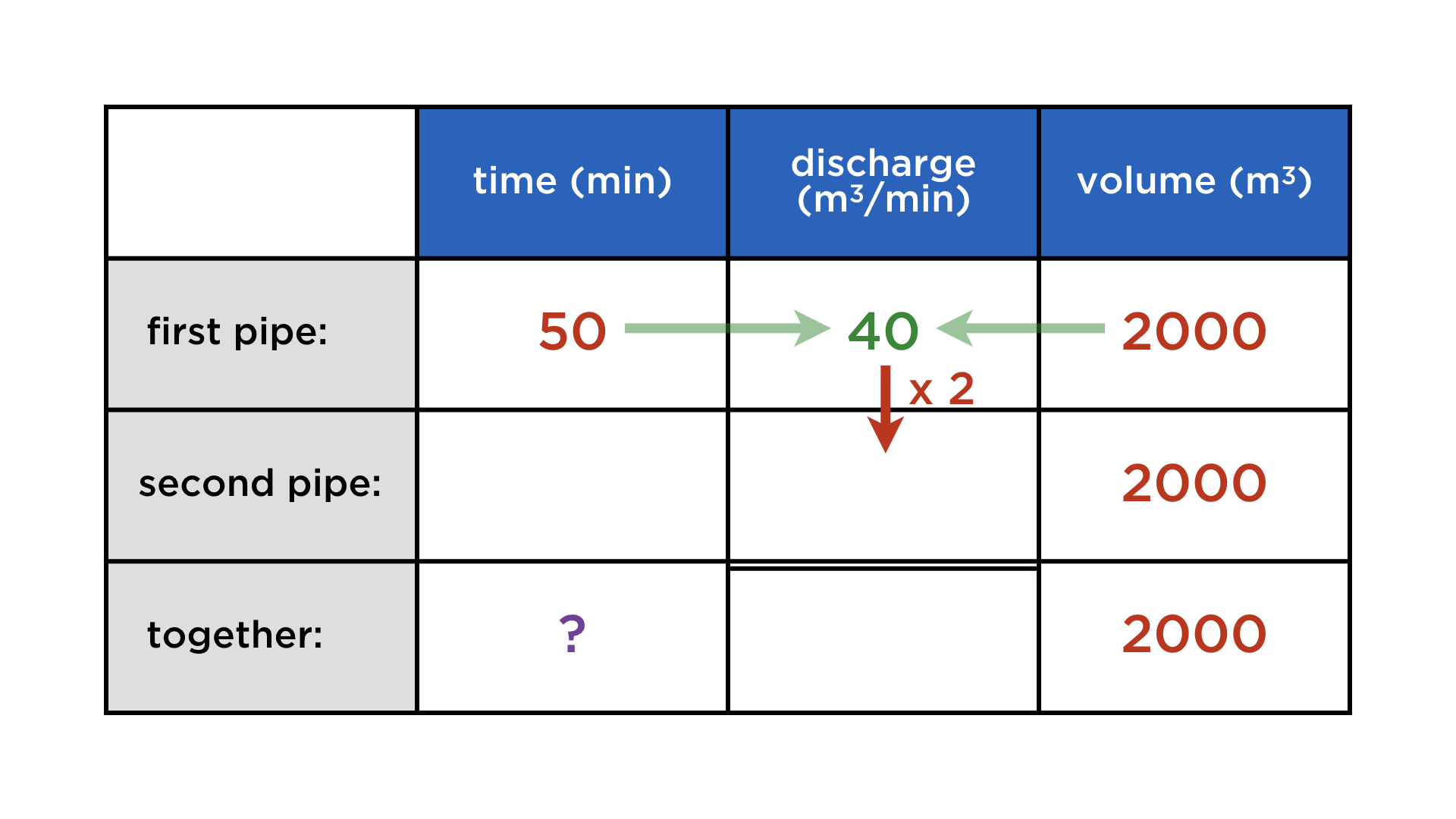
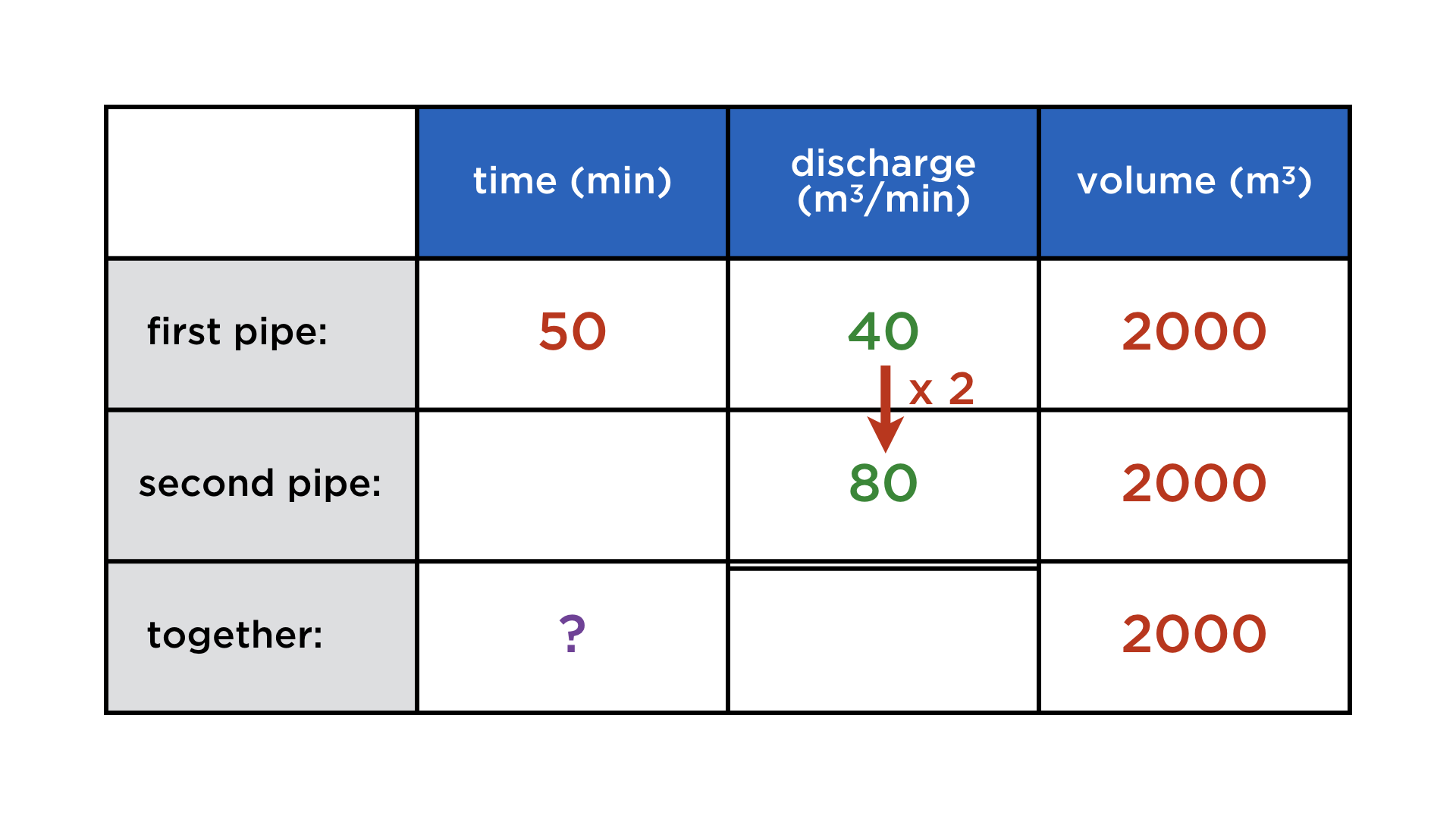
The incoming pipe of a sewage treatment plant can fill the sewage bassin (volume 2000 m³) in 50 min. A second pipe is being built, capable of carrying twice as much water per minute. How long will it take both pipes at once to fill the bassin?
Once more we are dealing with three quantities related by multiplication:
time (min) x discharge (m³/min) = volume (m³).
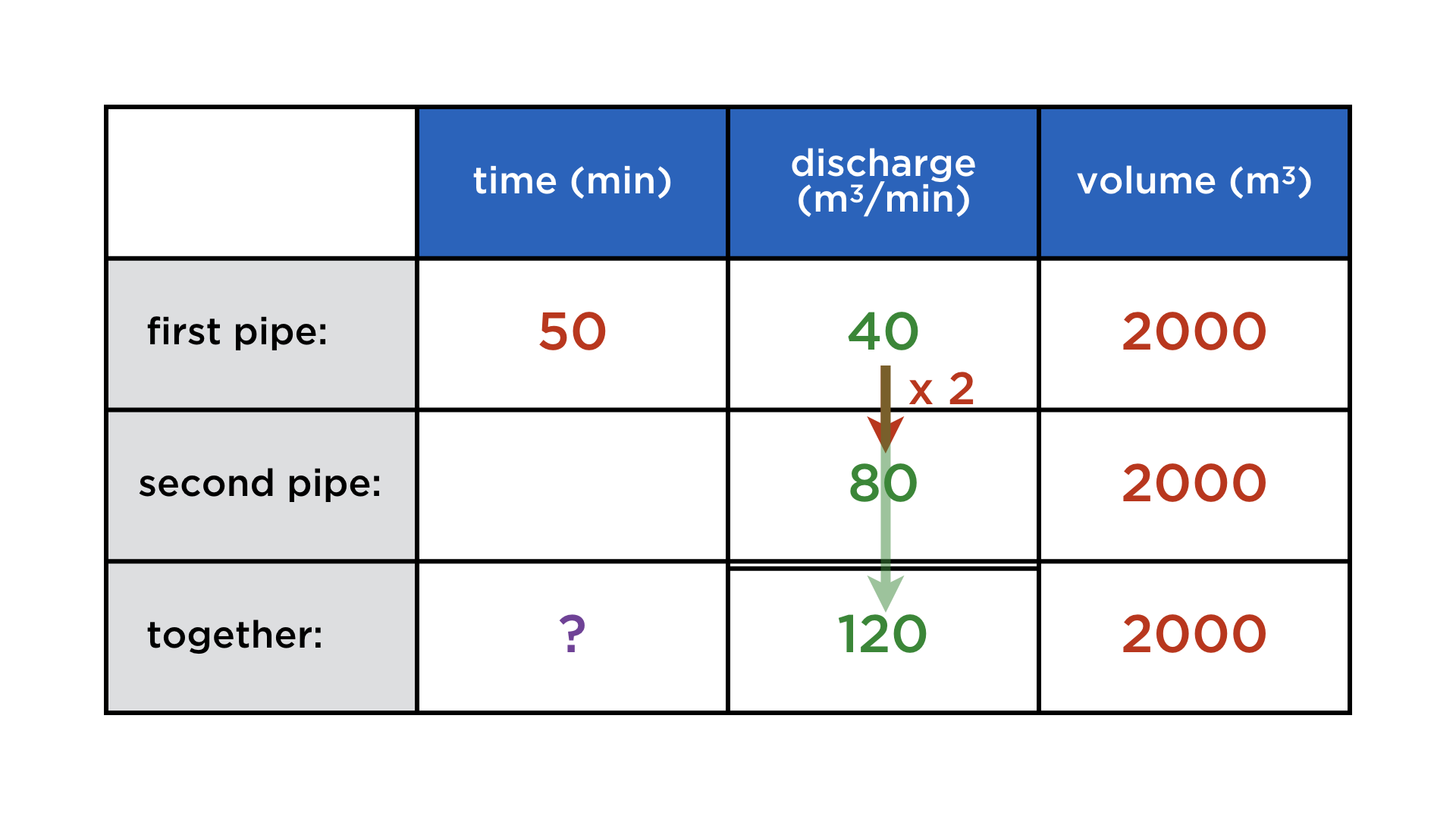
And once again, they occur in three variants: once for each pipe and once for both of them together. But there is a crucial difference to the previous problems: it is now the "rate", or "density", quantity that is additive, and none of the other two. In fact, the volume is the same in all three rows, since we compare three possible ways of performing the exact same task.
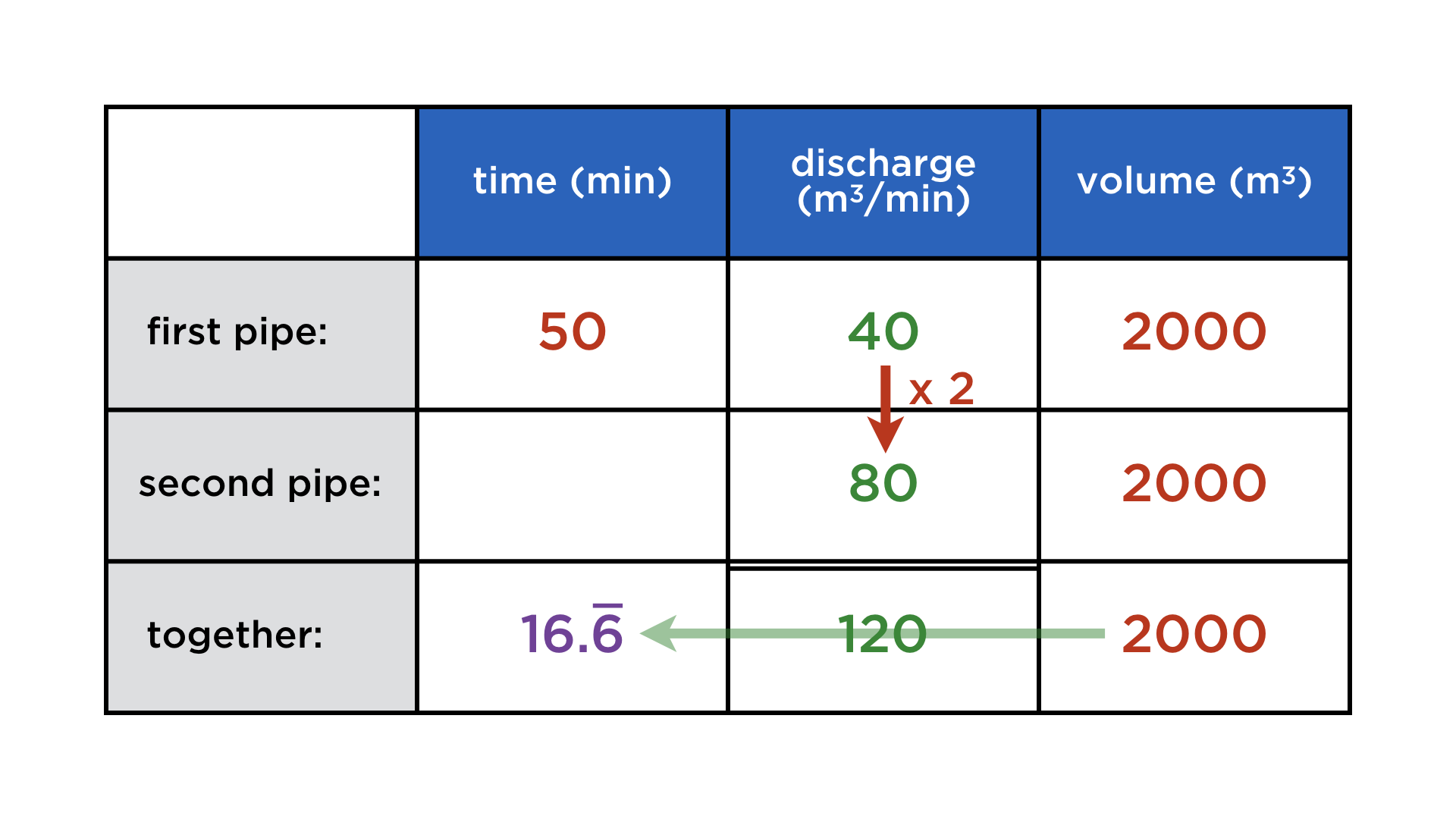
Keeping these changed relationships in mind, we can complete the table:
In fact, the bassin's volume is irrelevant, as one can check by algebra or common sense. This brings us to one of teachers's favourite problems.
WORK IT HARDER, MAKE IT BETTER
You knew this one would come.
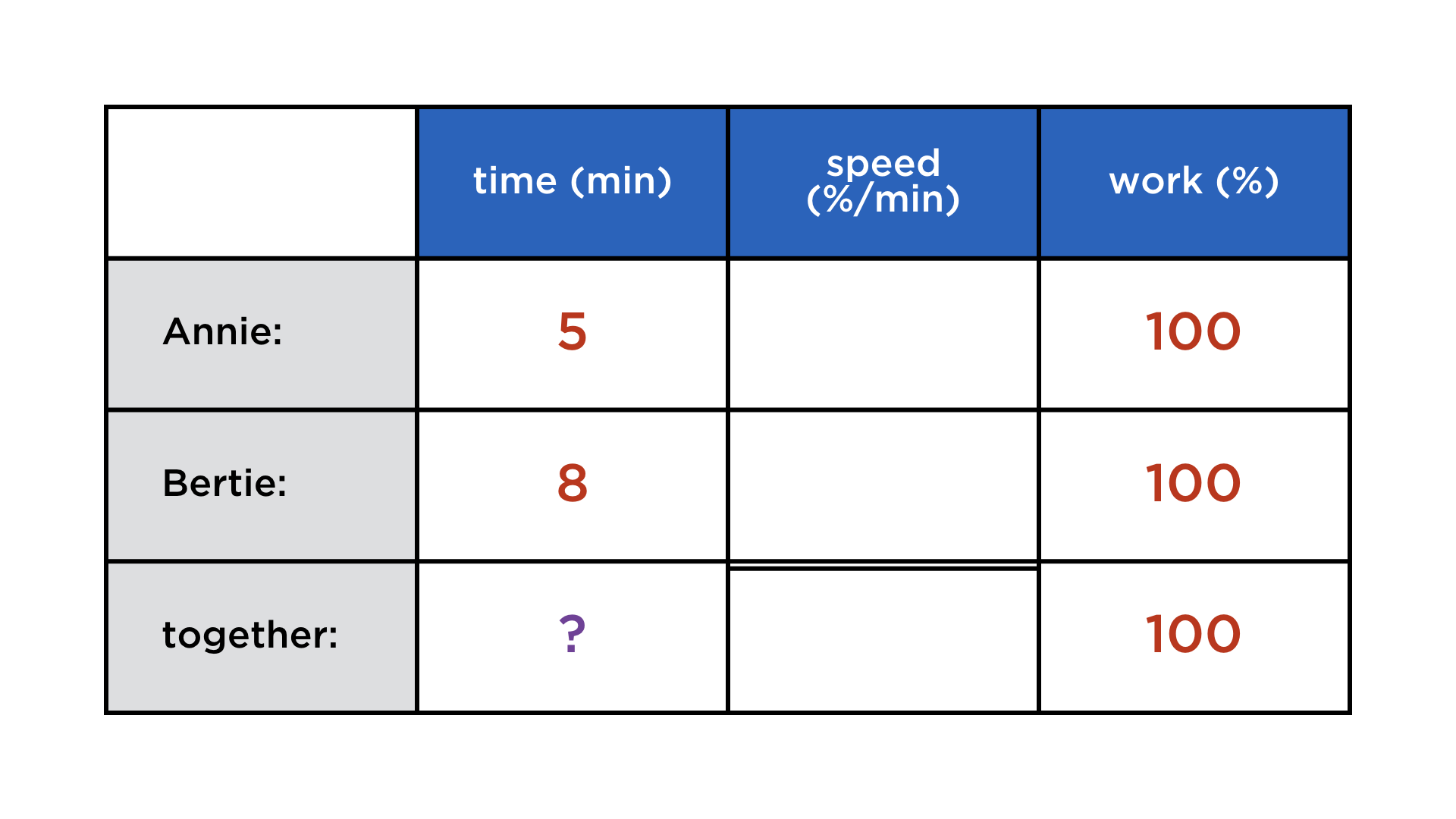
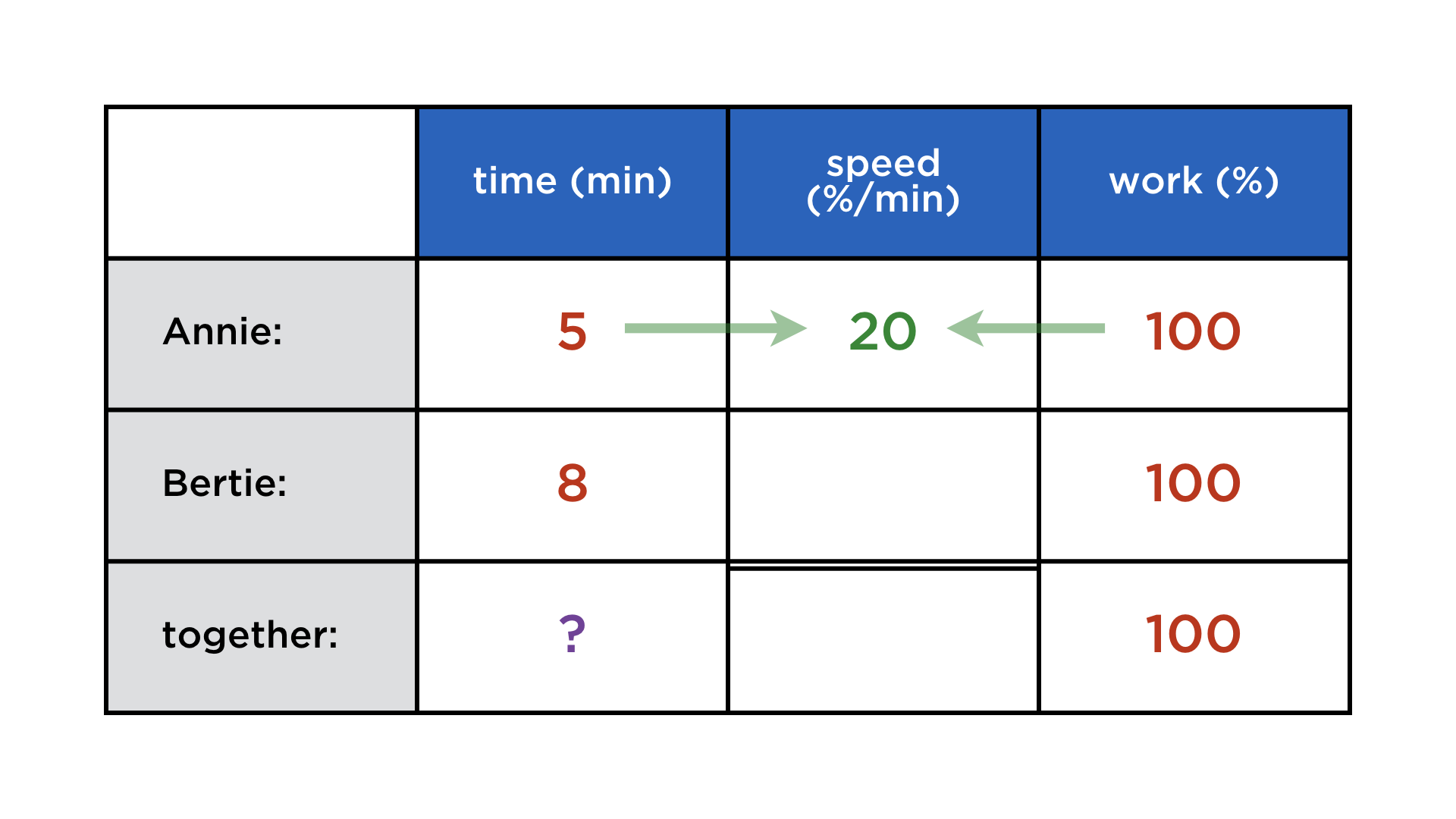
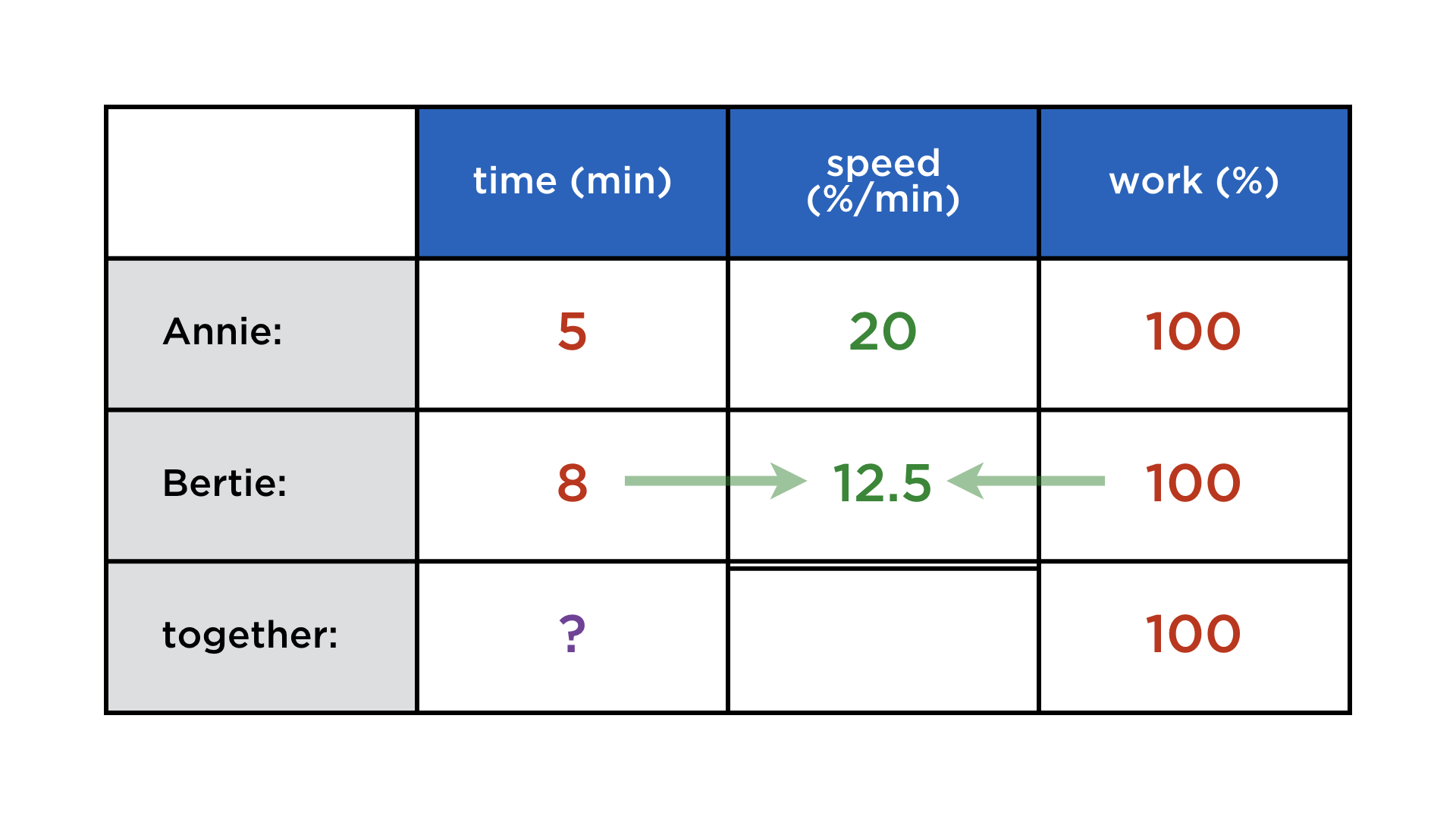
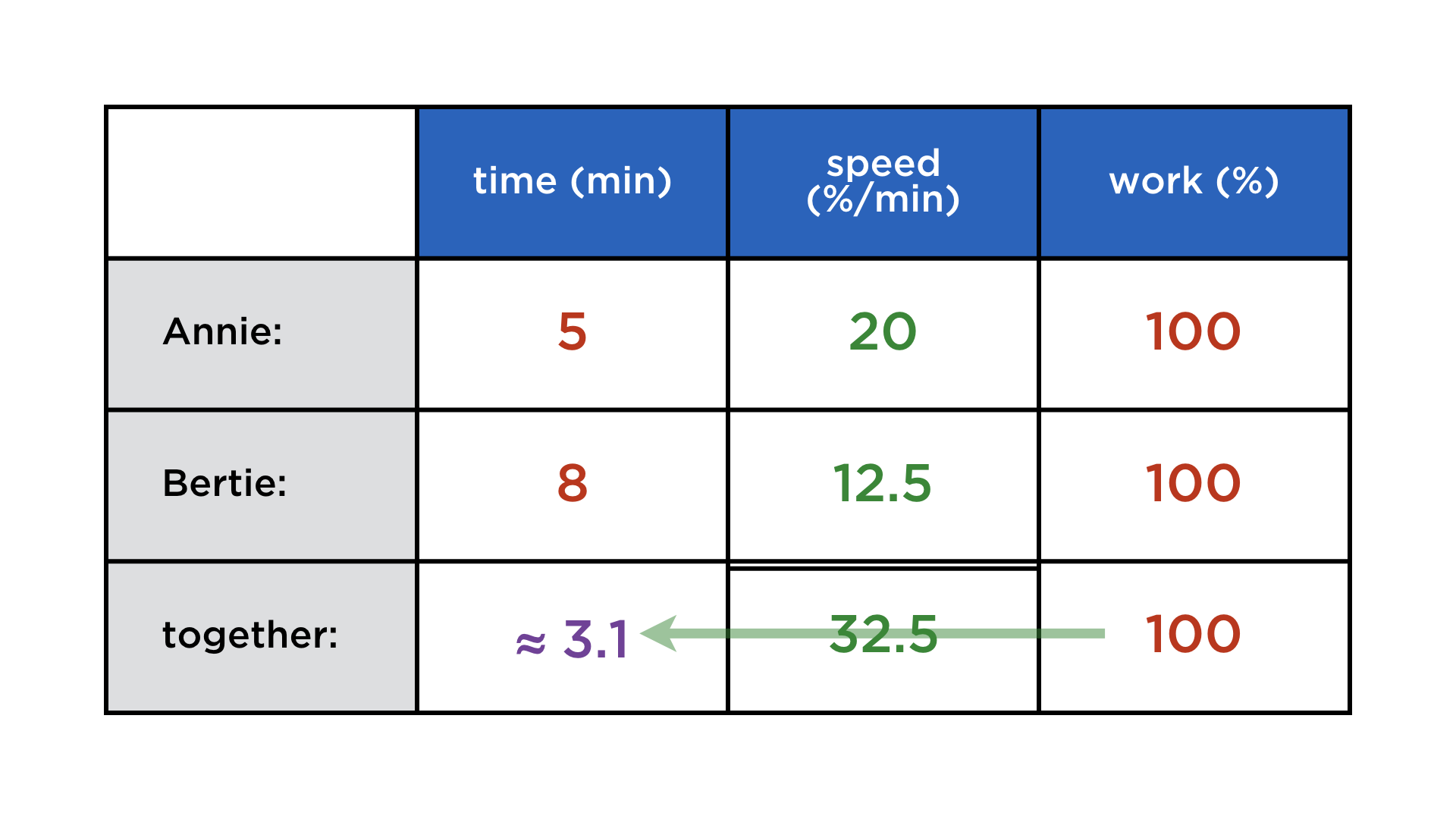
Annie takes 5 h to complete a certain task, Bertie needs 8 h for the same work. How long will they take working together?
Of course, this depends on the kind of task at hand. But we are in math class here and thus there are no other kinds of work than the continuously divisible kind, such as digging holes and painting fences. The formulation of the problem is abstract enough that many students do not realize the wrongness of simply adding (or subtracting) the durations. In a tabular setup, and with the preparation of volume-filling problems, it becomes much clearer which quantities can be added and which ones cannot. Also, the need for an arbitrary number for the total workload can be addressed more clearly when faced with a table that is too sparse to complete, but otherwise analogous to the previous problem:
All these problems could be solved purely arithmetically. In part II, we will see how the table method extends to problems requiring an equation in an unknown. It is astonishing how many textbook word problems fit one of these basic tables, or simple variations of them – so stay tuned!
ADDENDUM
Here are a few more word problems that can be solved with the table method.
1. A group of people is taking the train. The tickets costs 84 € per person, unless they have a half-fare card. The total price for the trip is 3990 €. If 15 people of the group carry a half-fare card, how many are in the group?
2. A volume of 50 g of concentrated hydrochloric acid (HCl, 90 % concentration) is being mixed with 200 g of more diluted HCl (15 % concentration). As the resulting solution is still too strong, it is being diluted with water. How much water does one have to add to achieve a concentration of 5 %?
3. A stadium is being fitted with 5500 additional seats and a second exit. The old exit could empty the whole stadium (22 000 sports fans) in 44 min. The new, wider exit can empty the new stadium by itself in half the time. How long will it take to evacuate using both exits together?
4. A swimming pool can be filled in 45 min and drained in 50 min. How long will it take to fill if the janitor forgets to close the drain?