Why is math so hard (on a computer)?

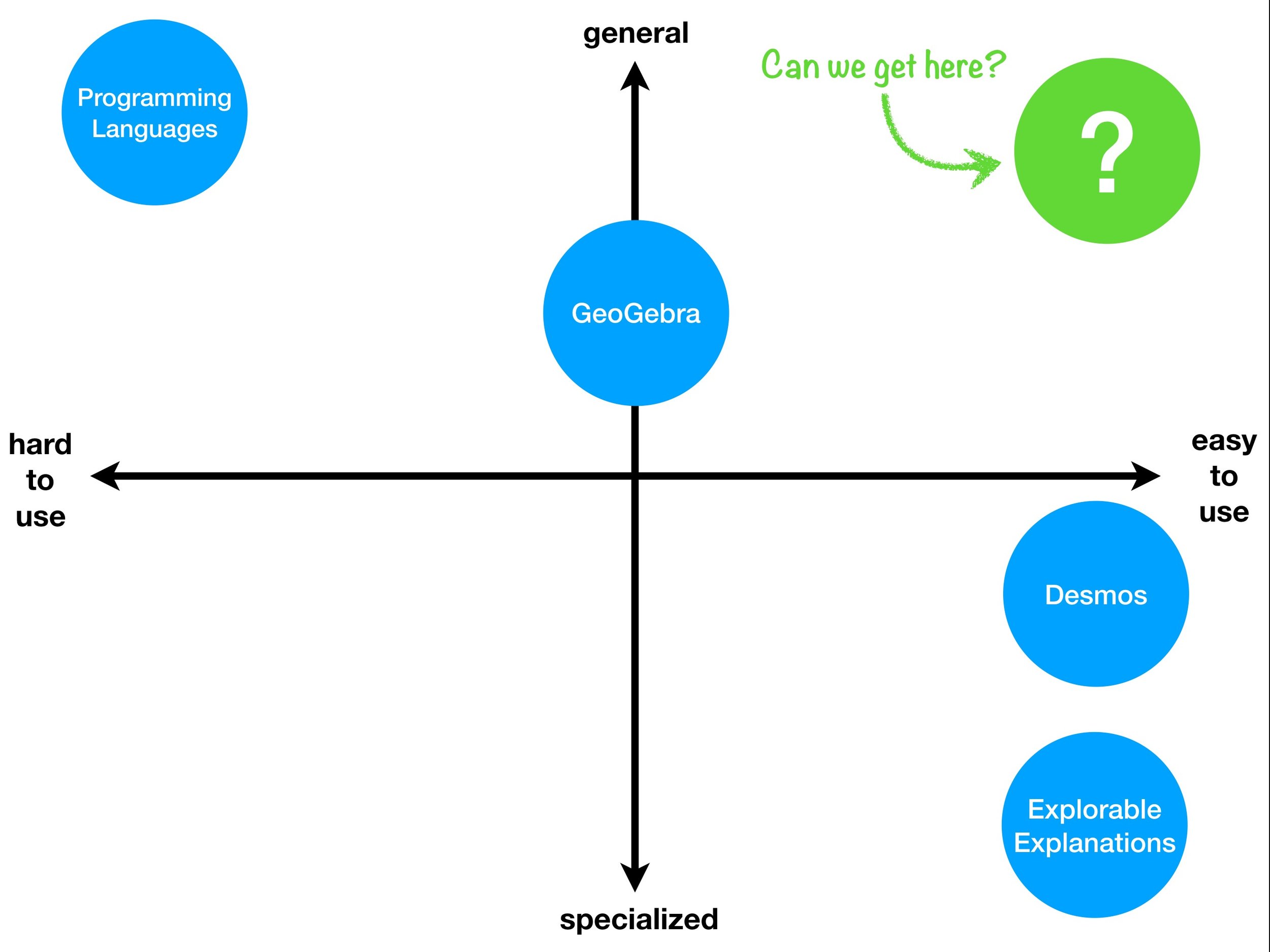
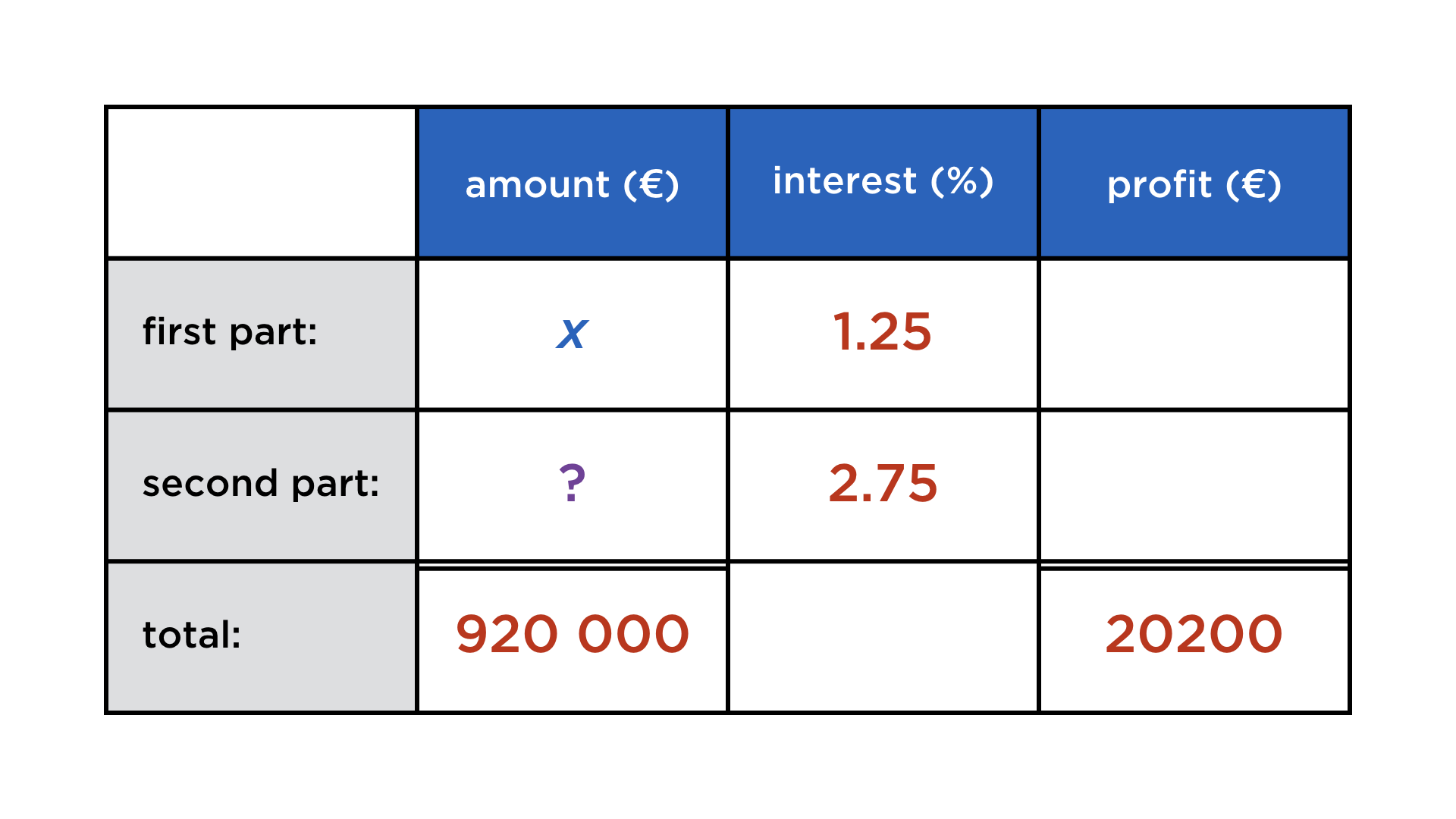
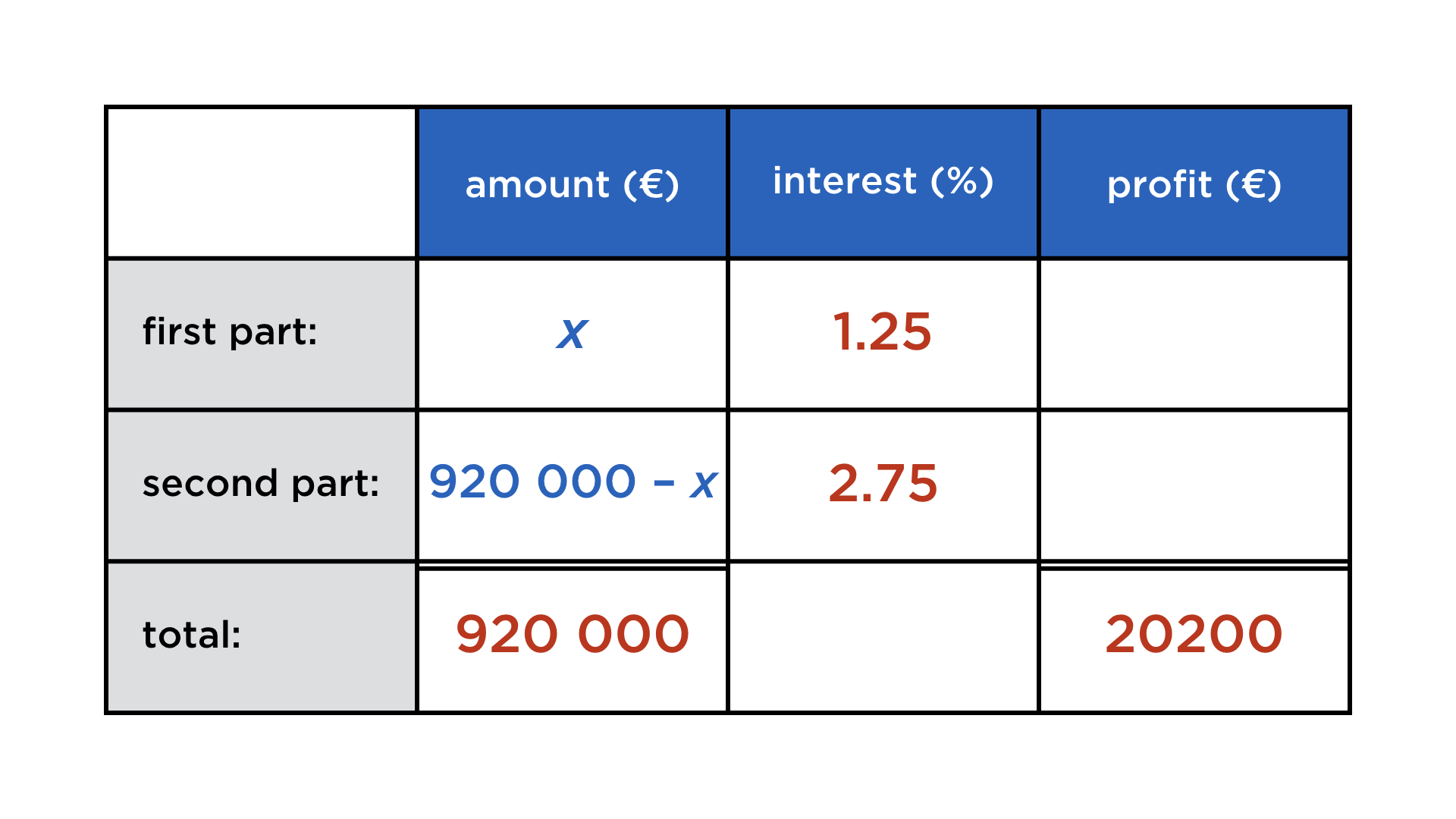
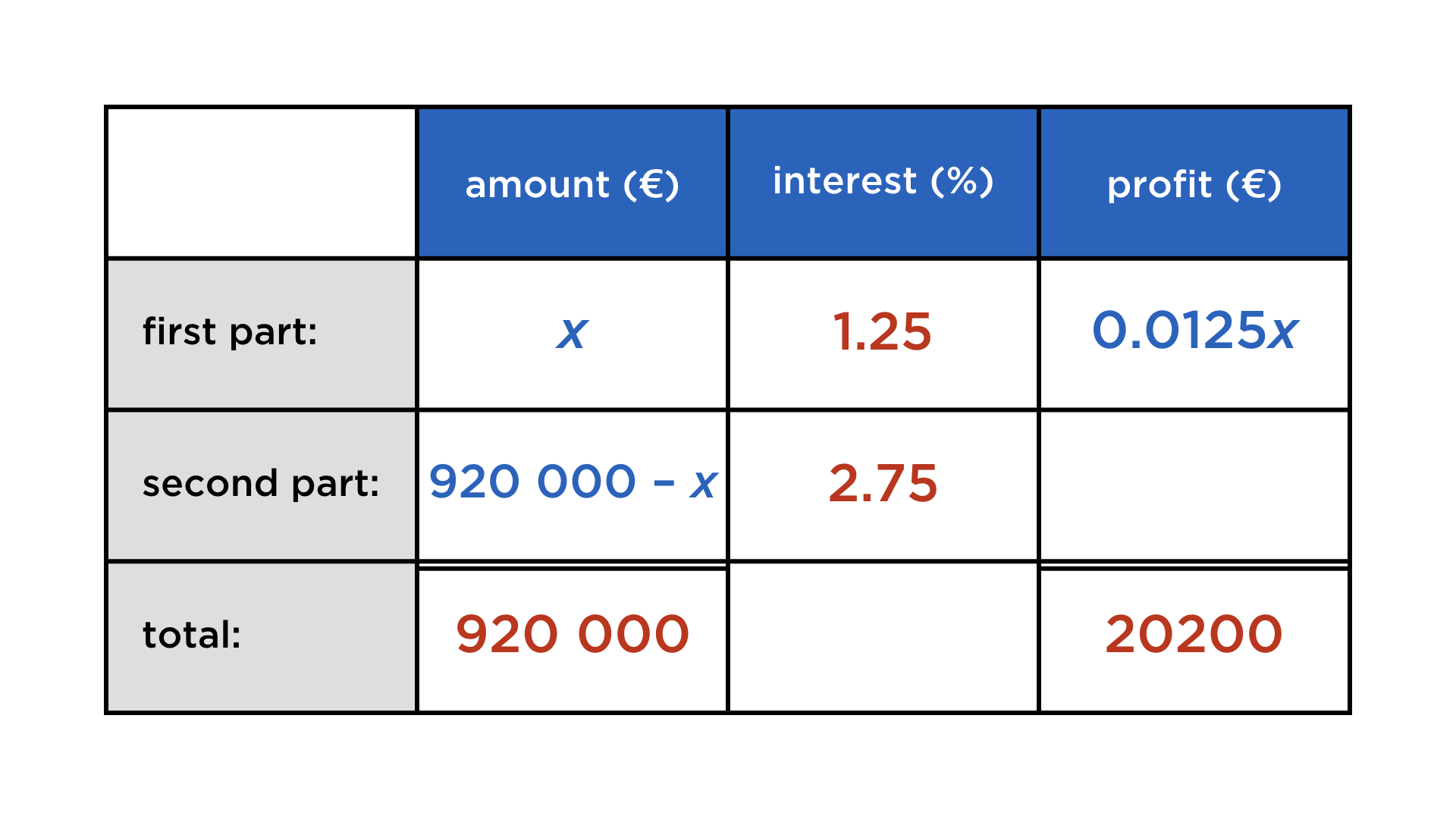
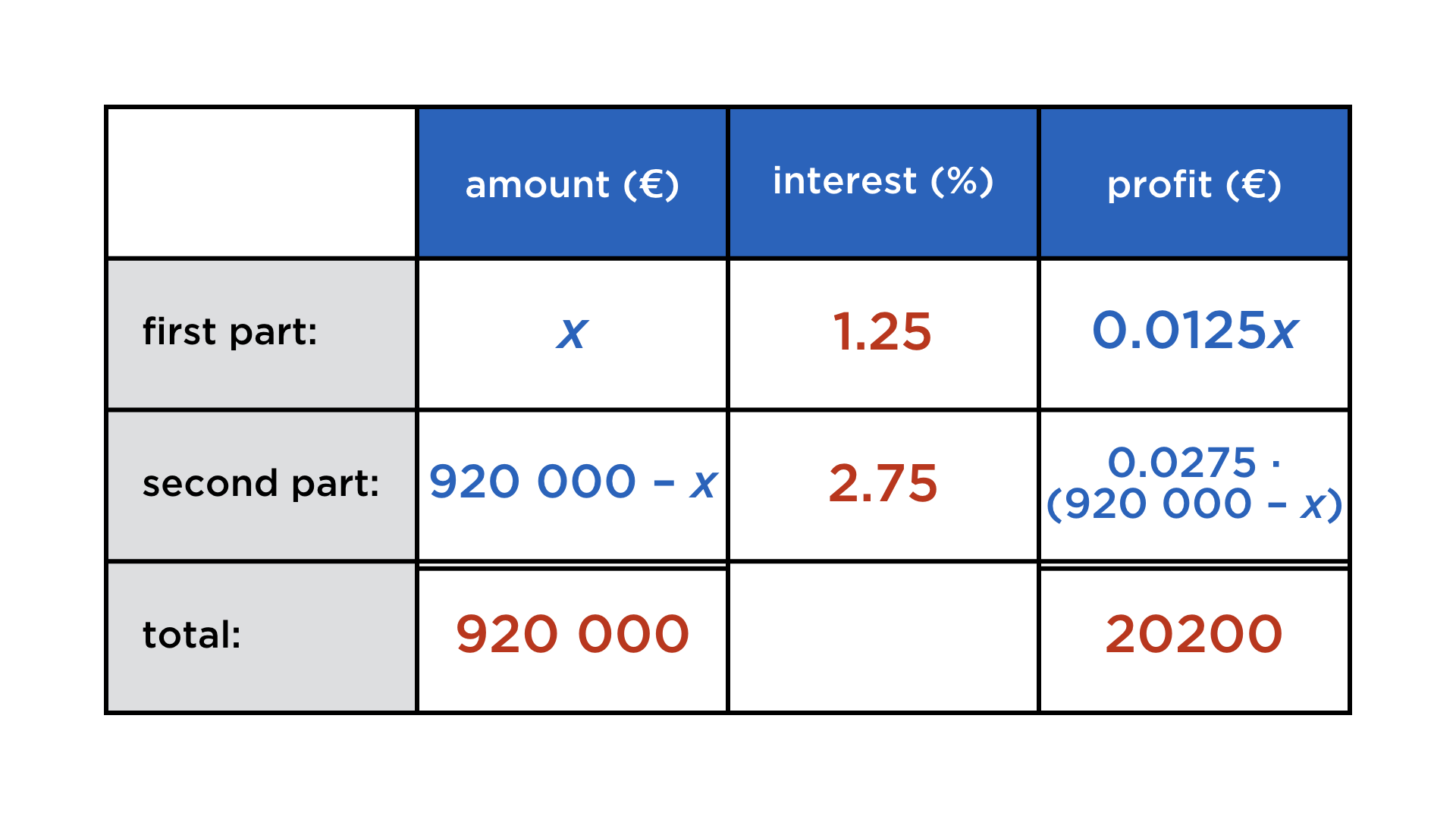
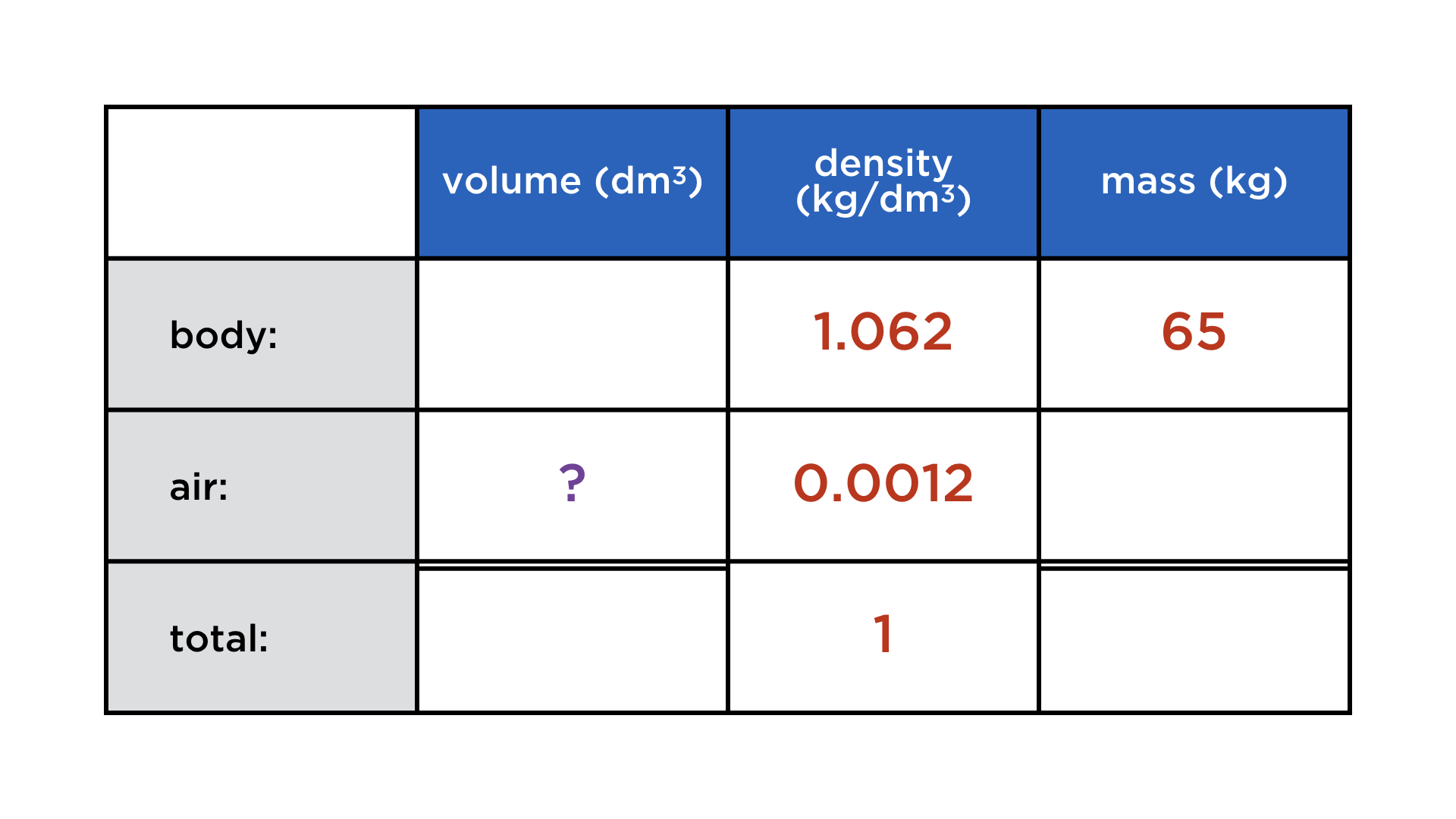
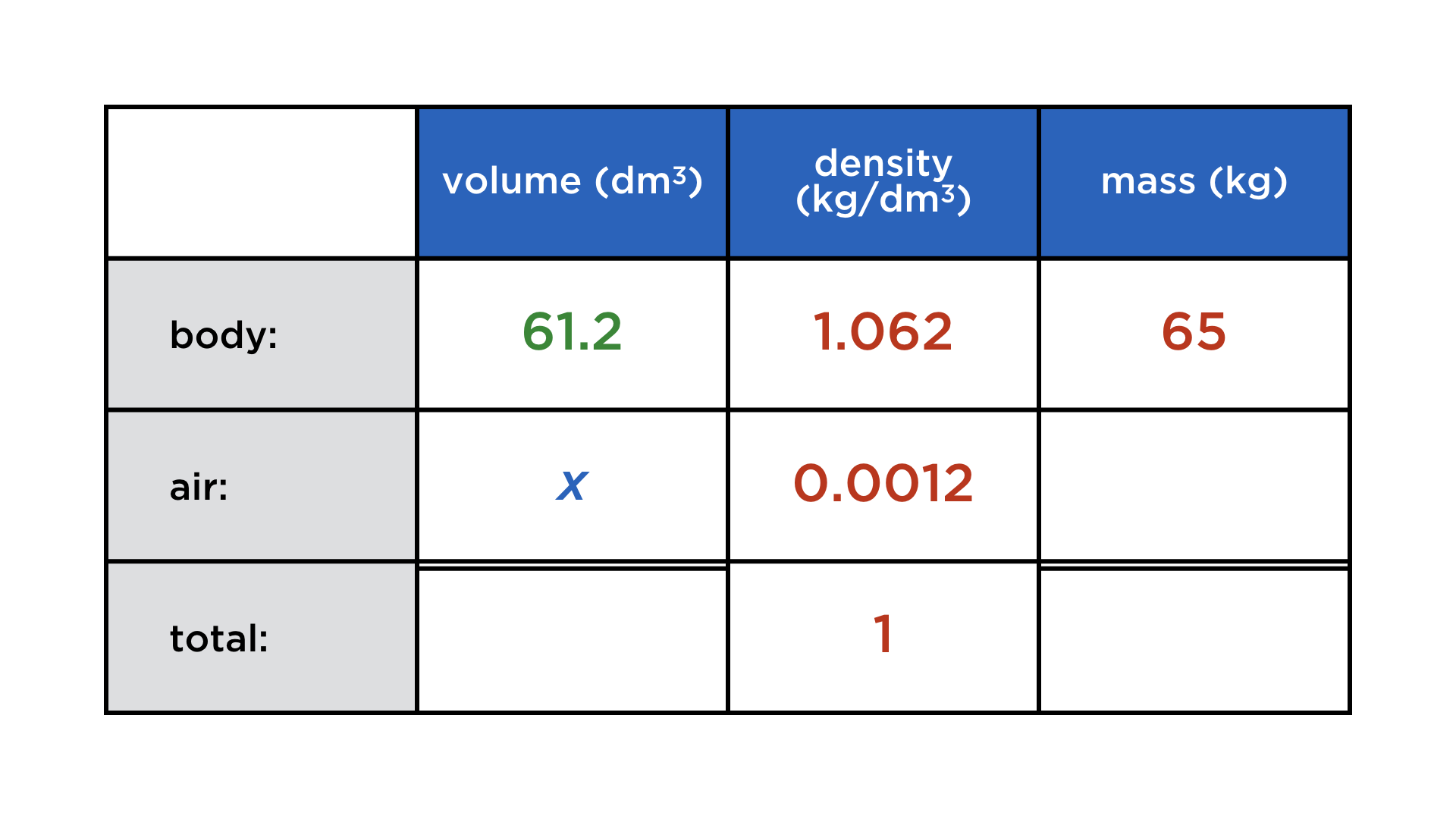
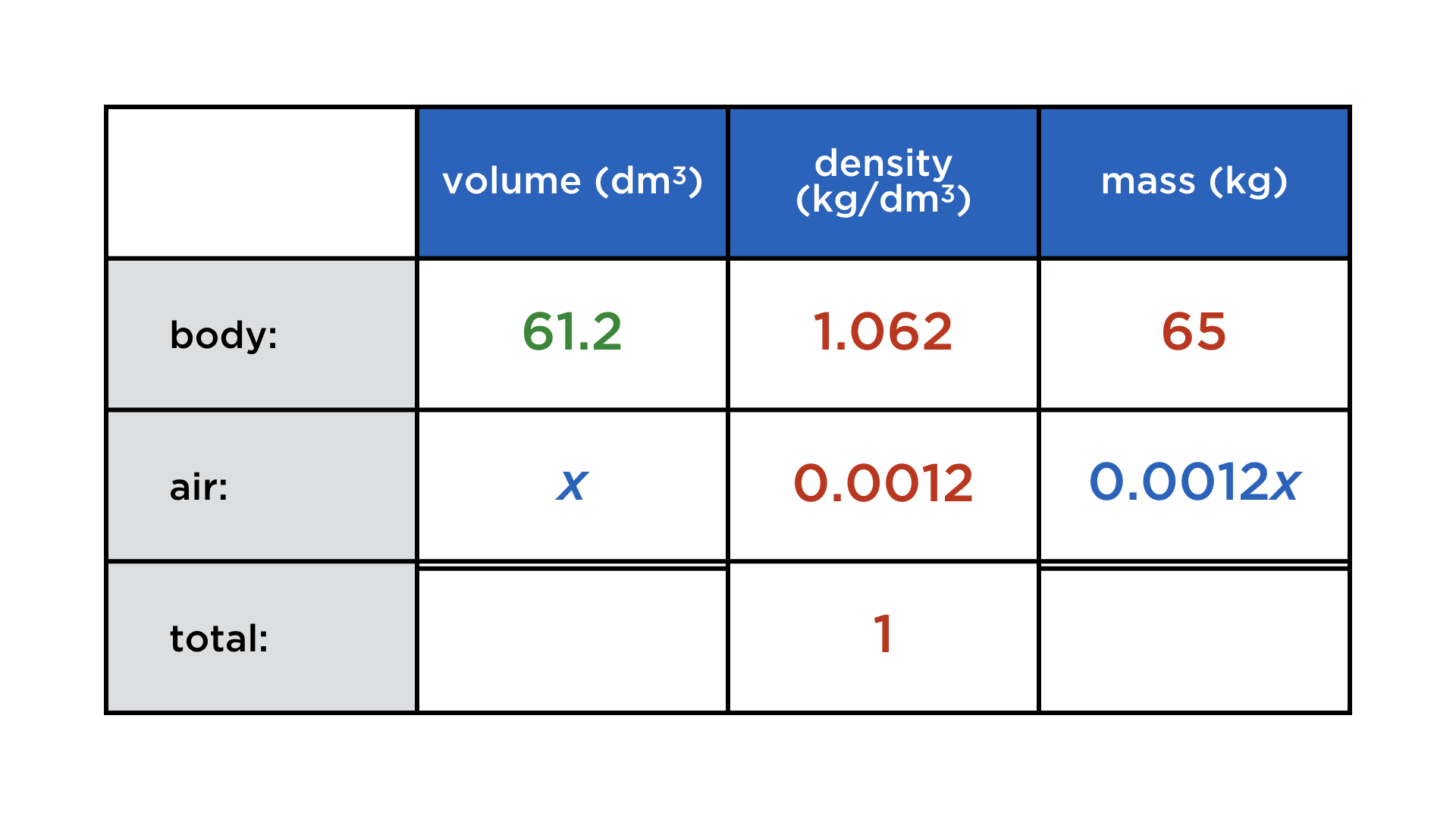
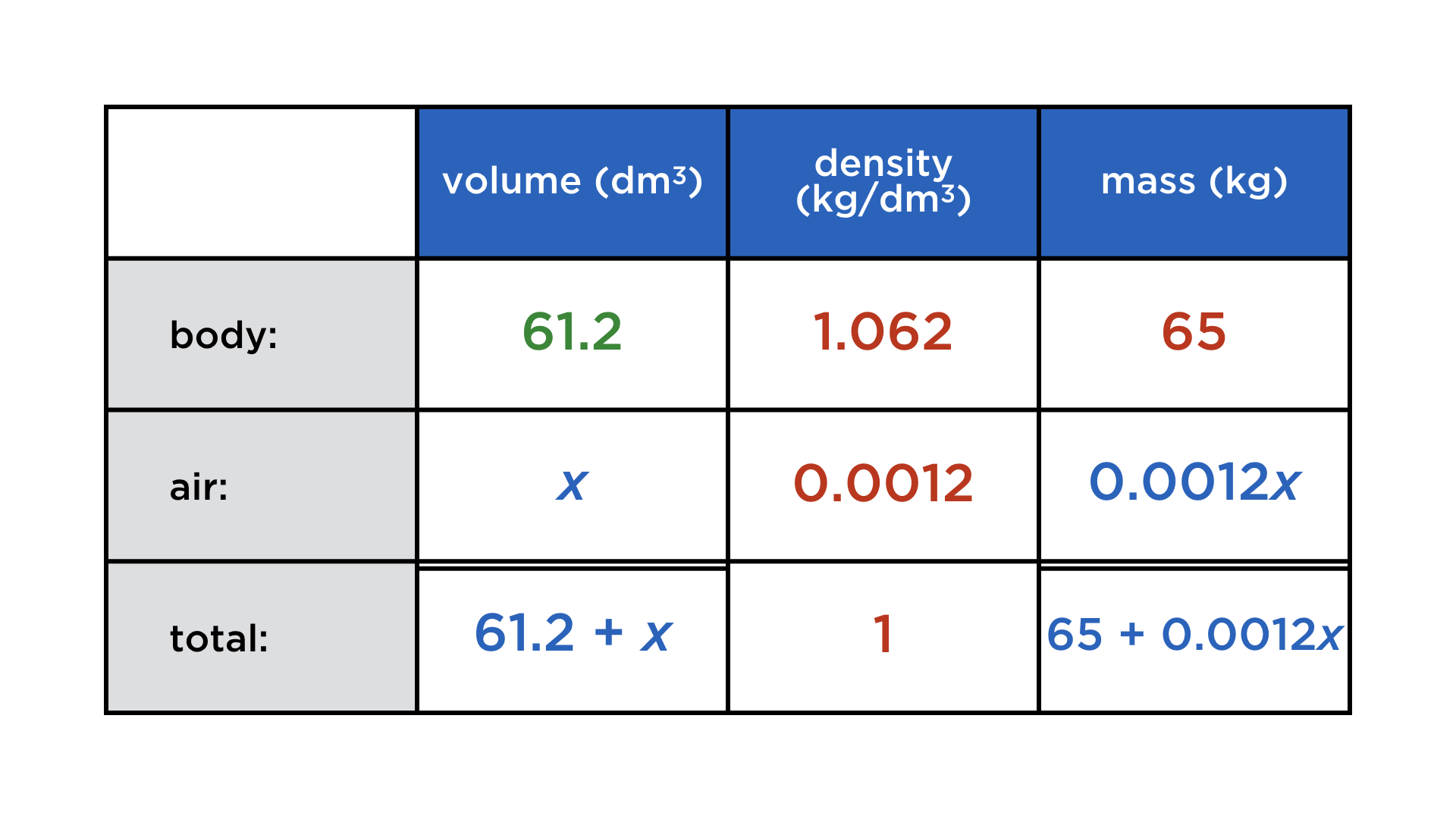
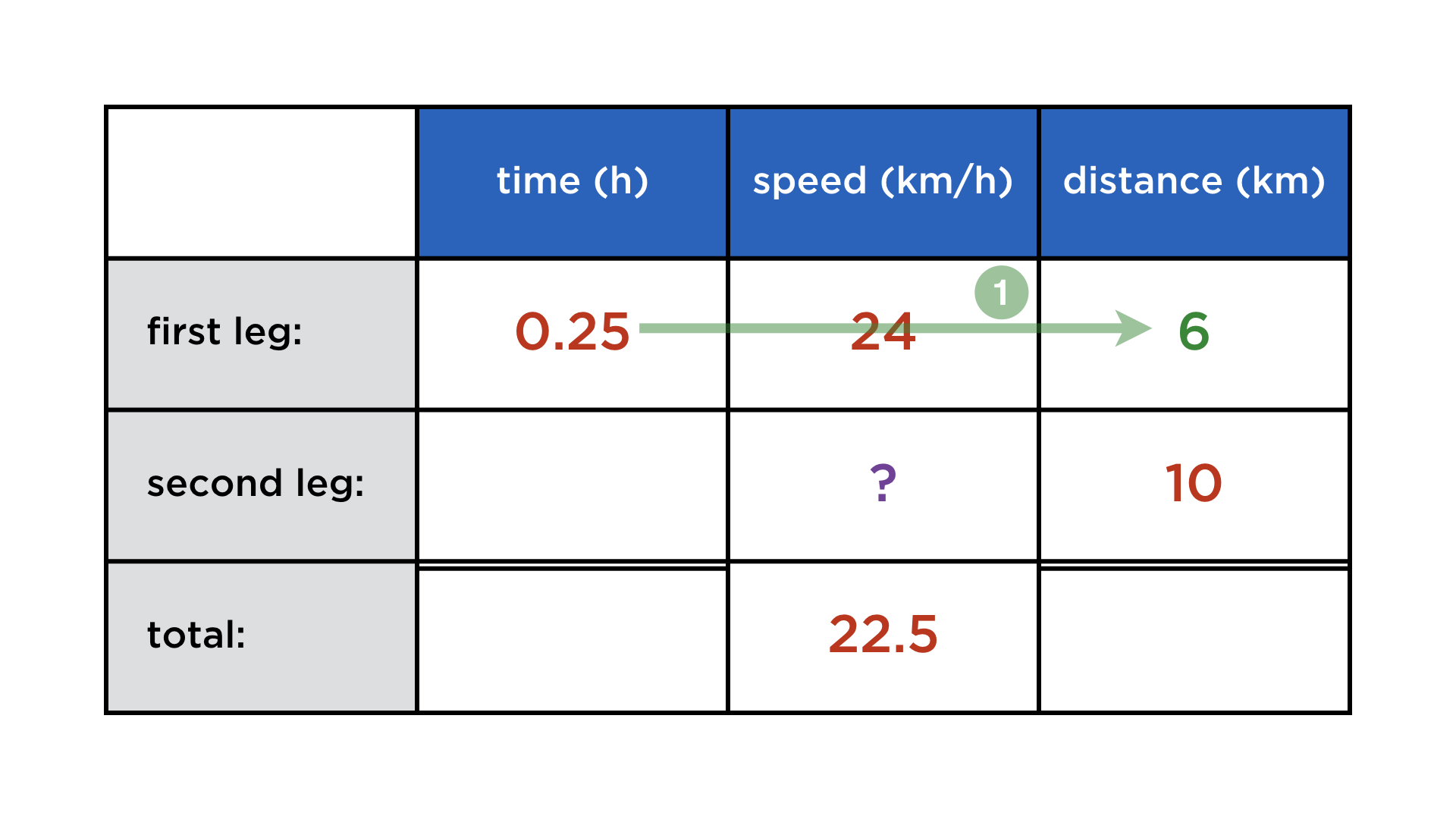
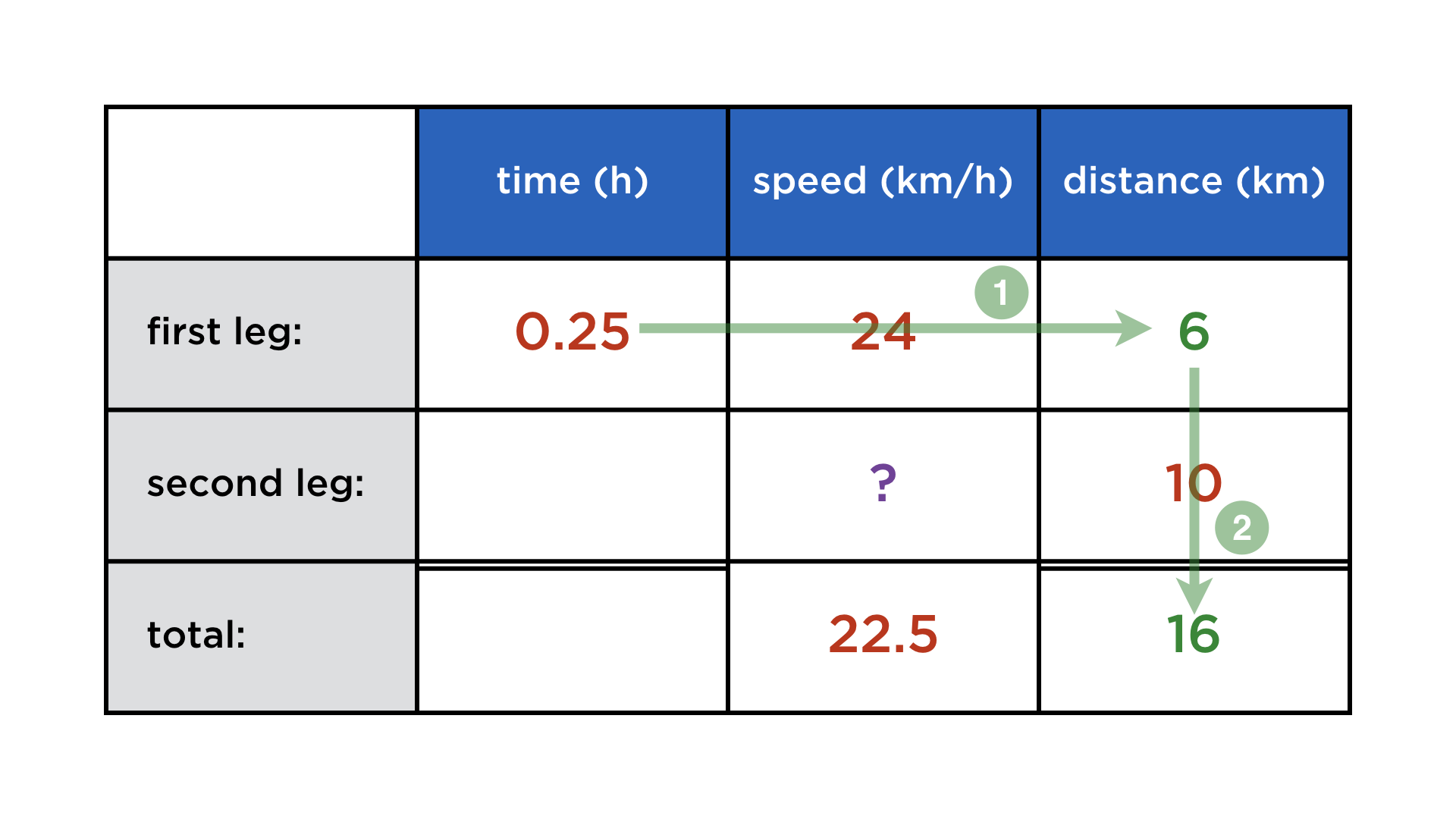
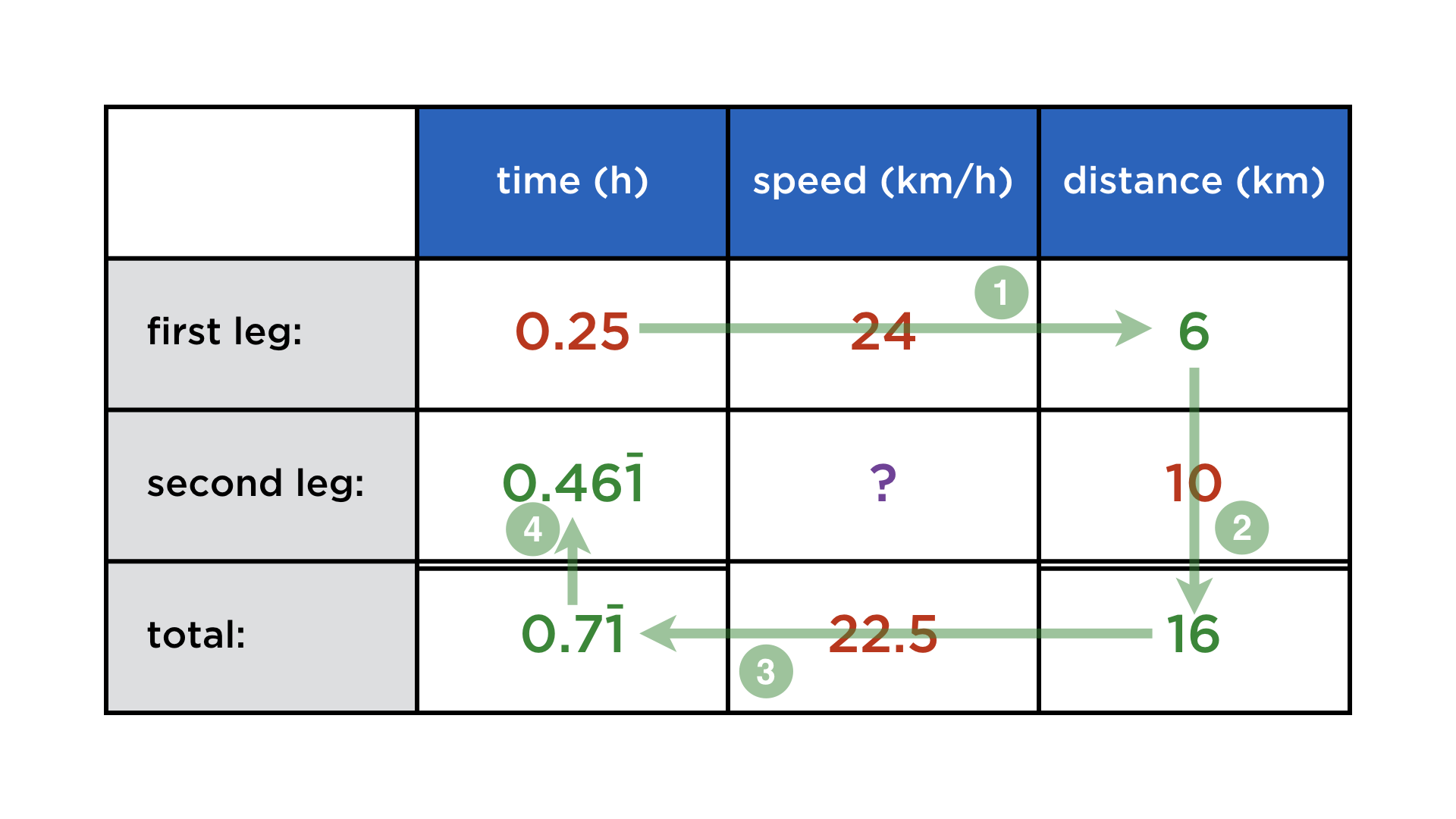
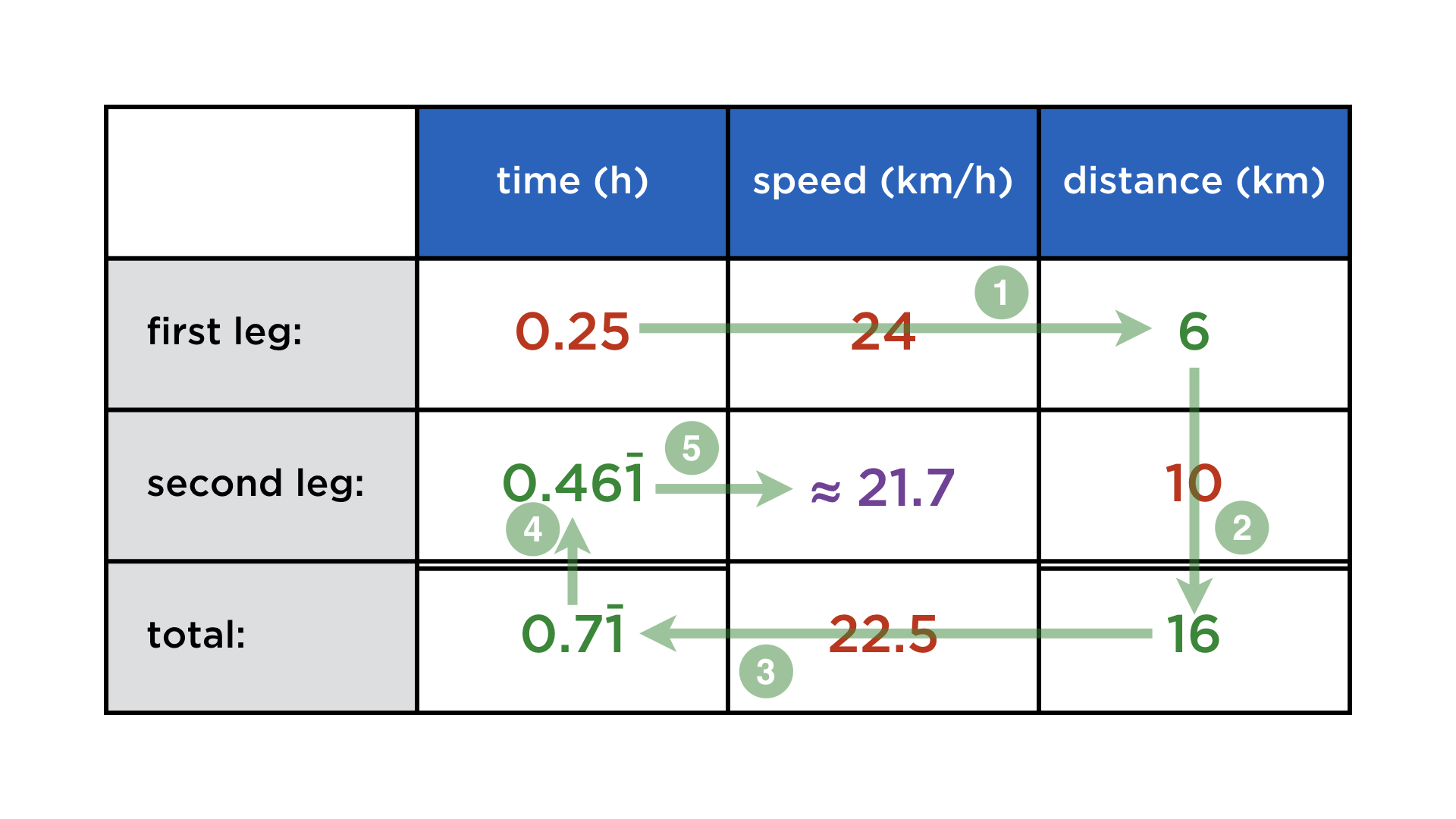
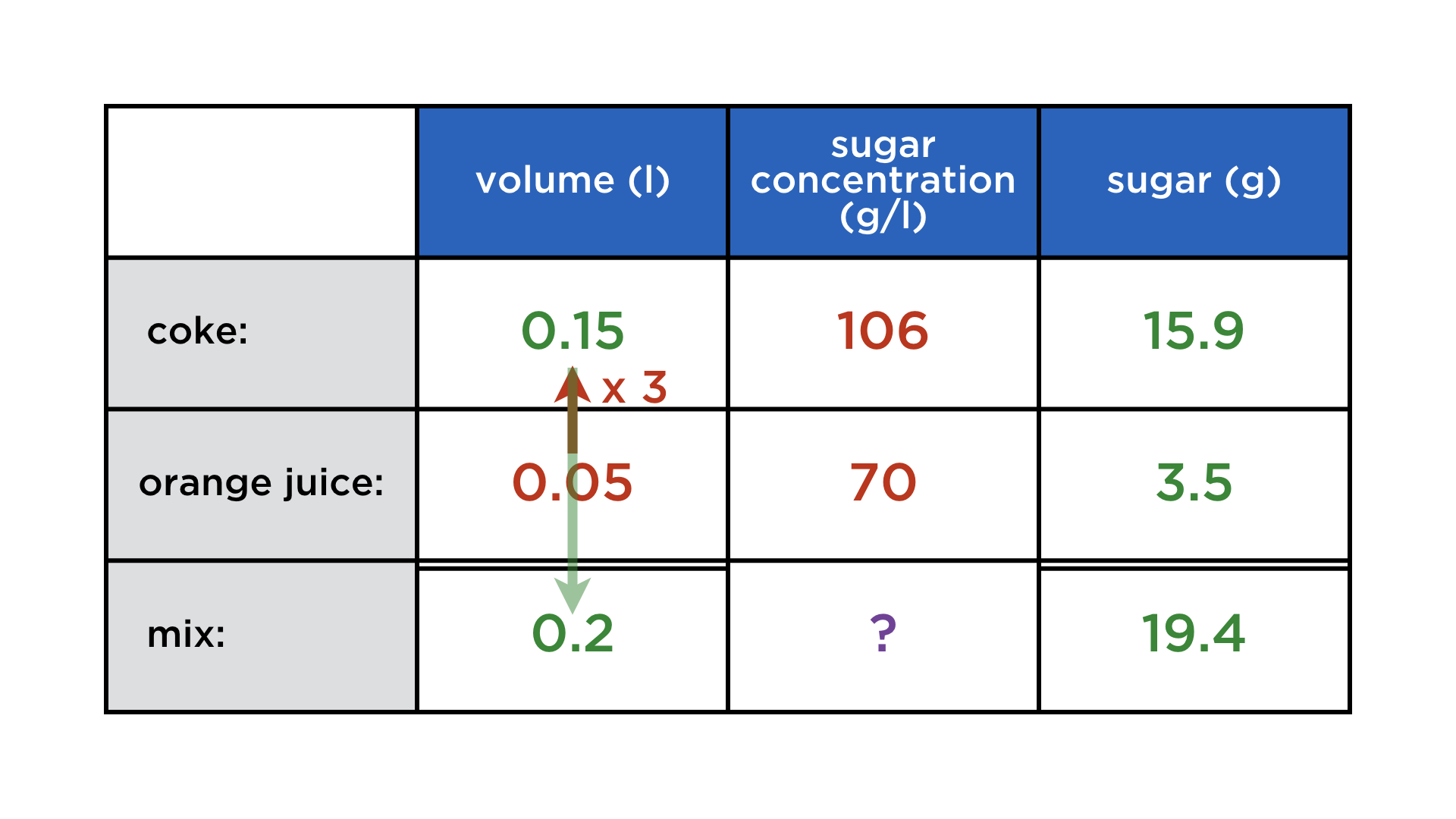
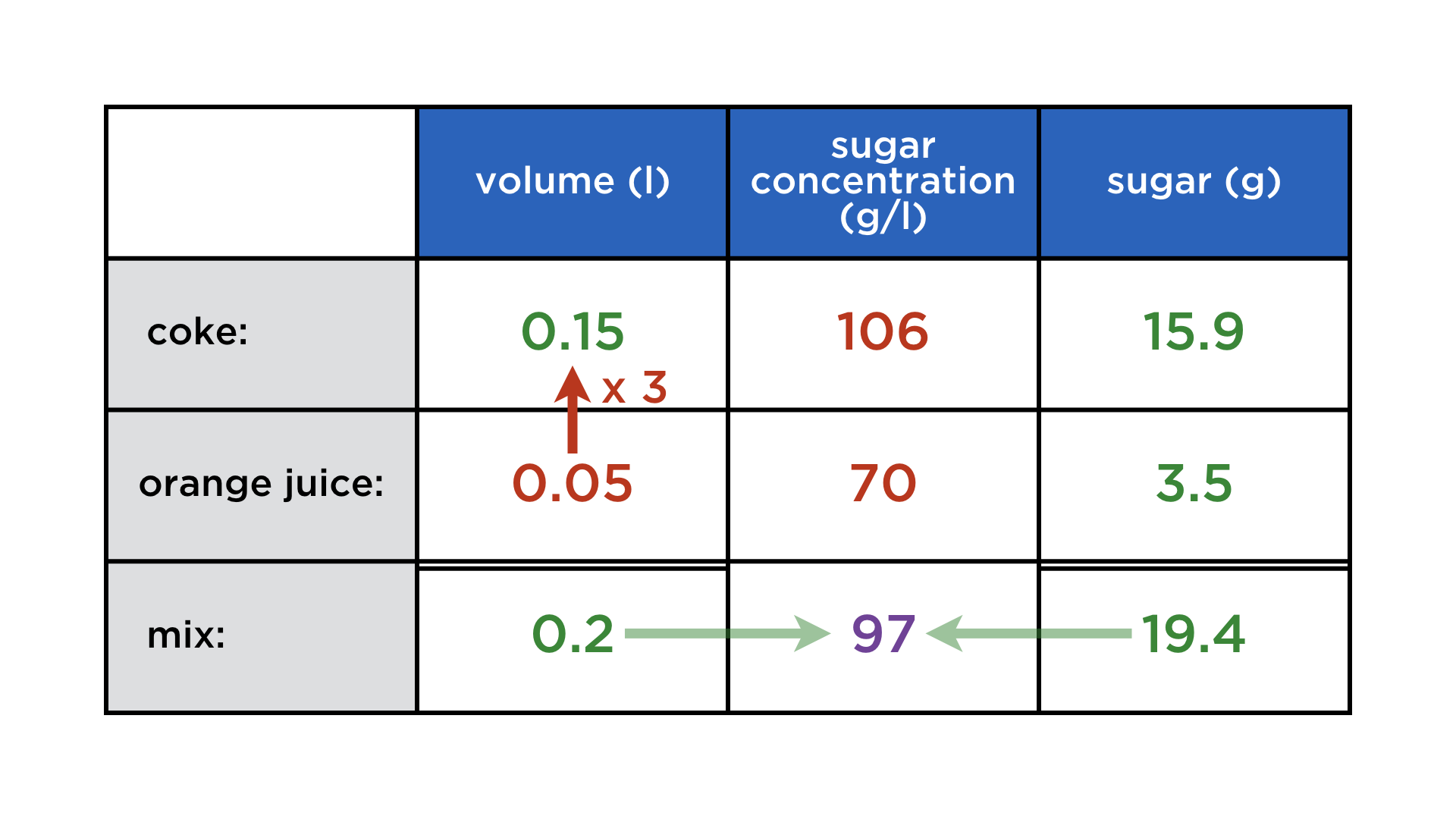
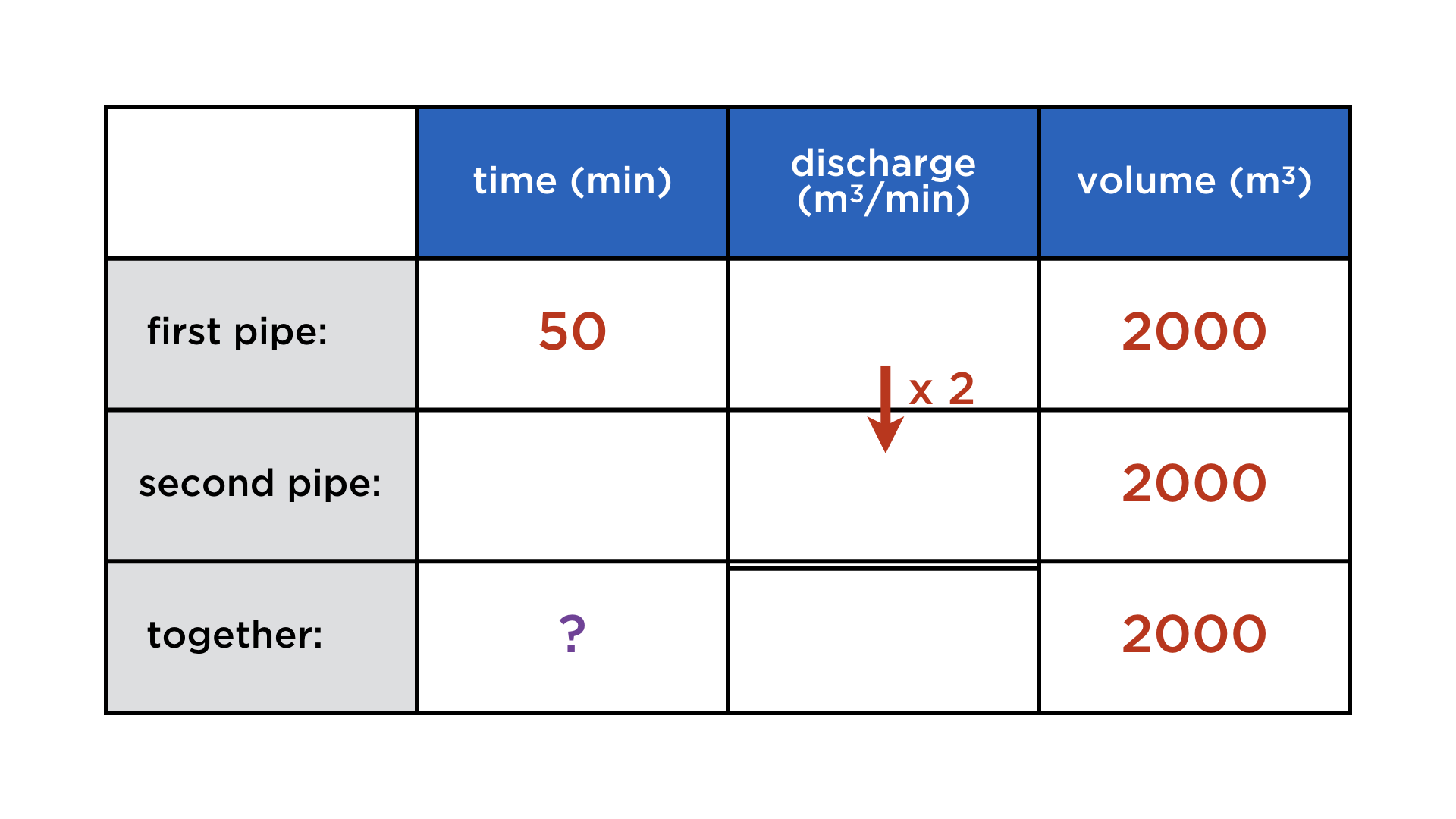
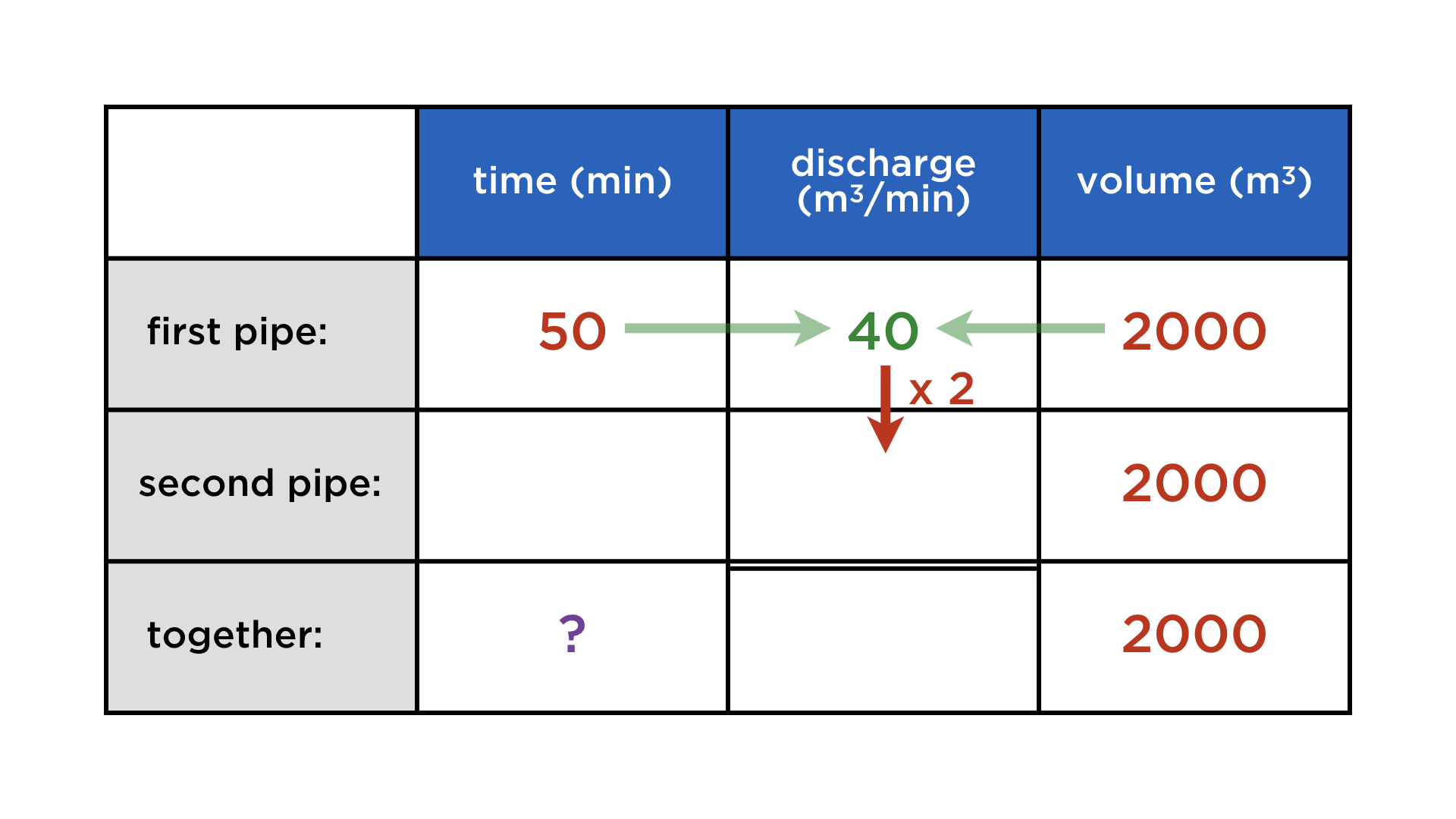
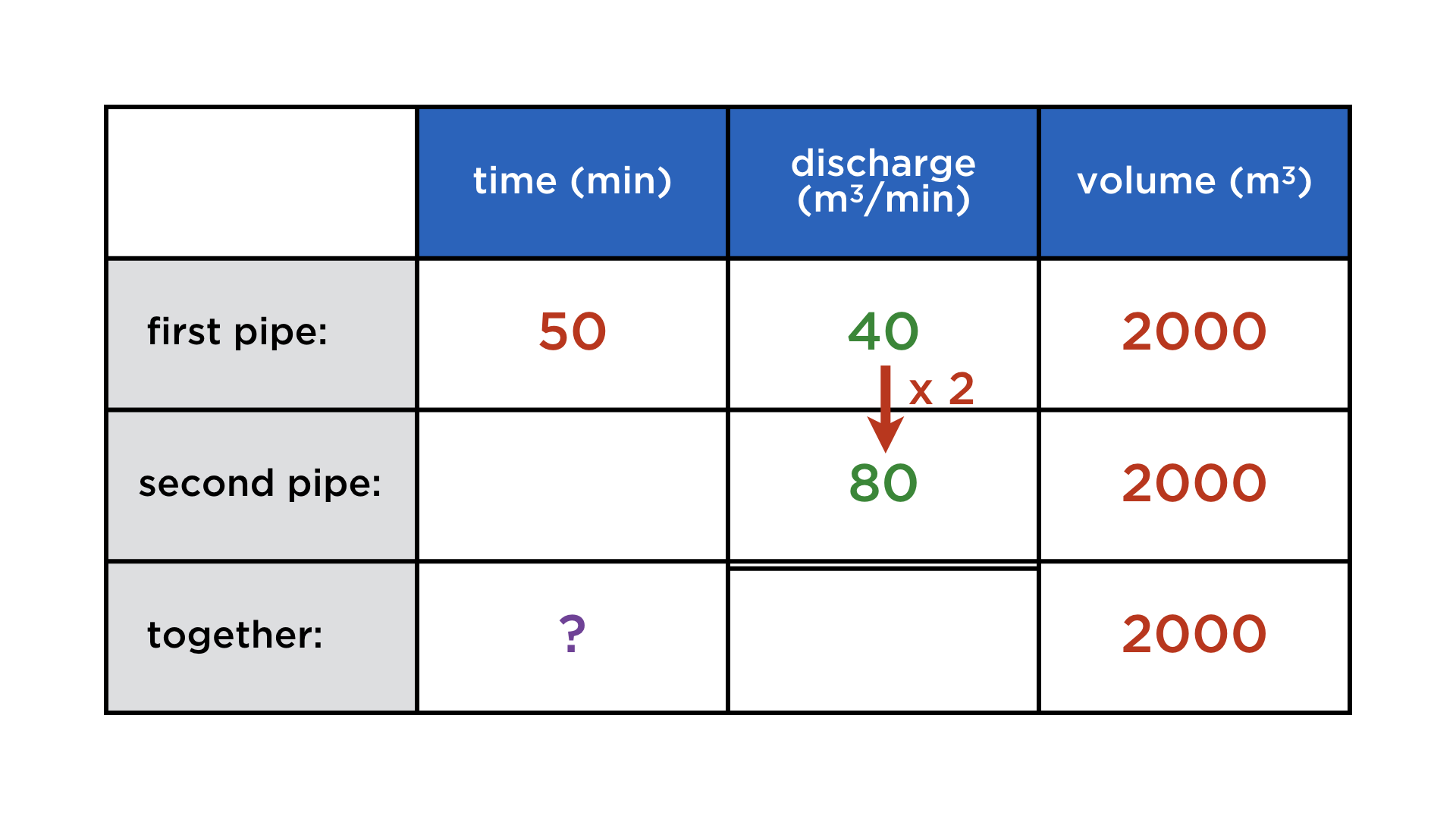
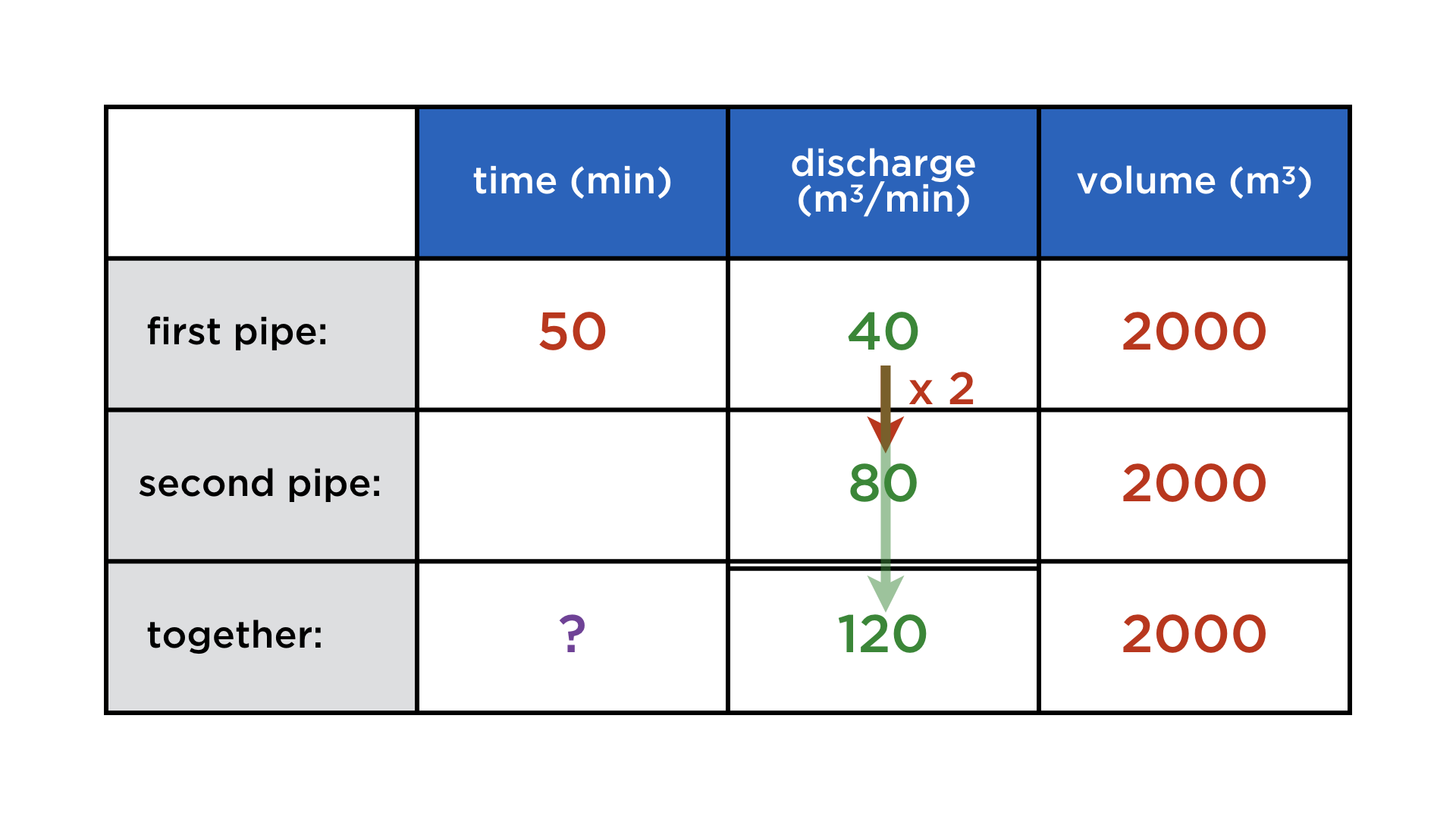
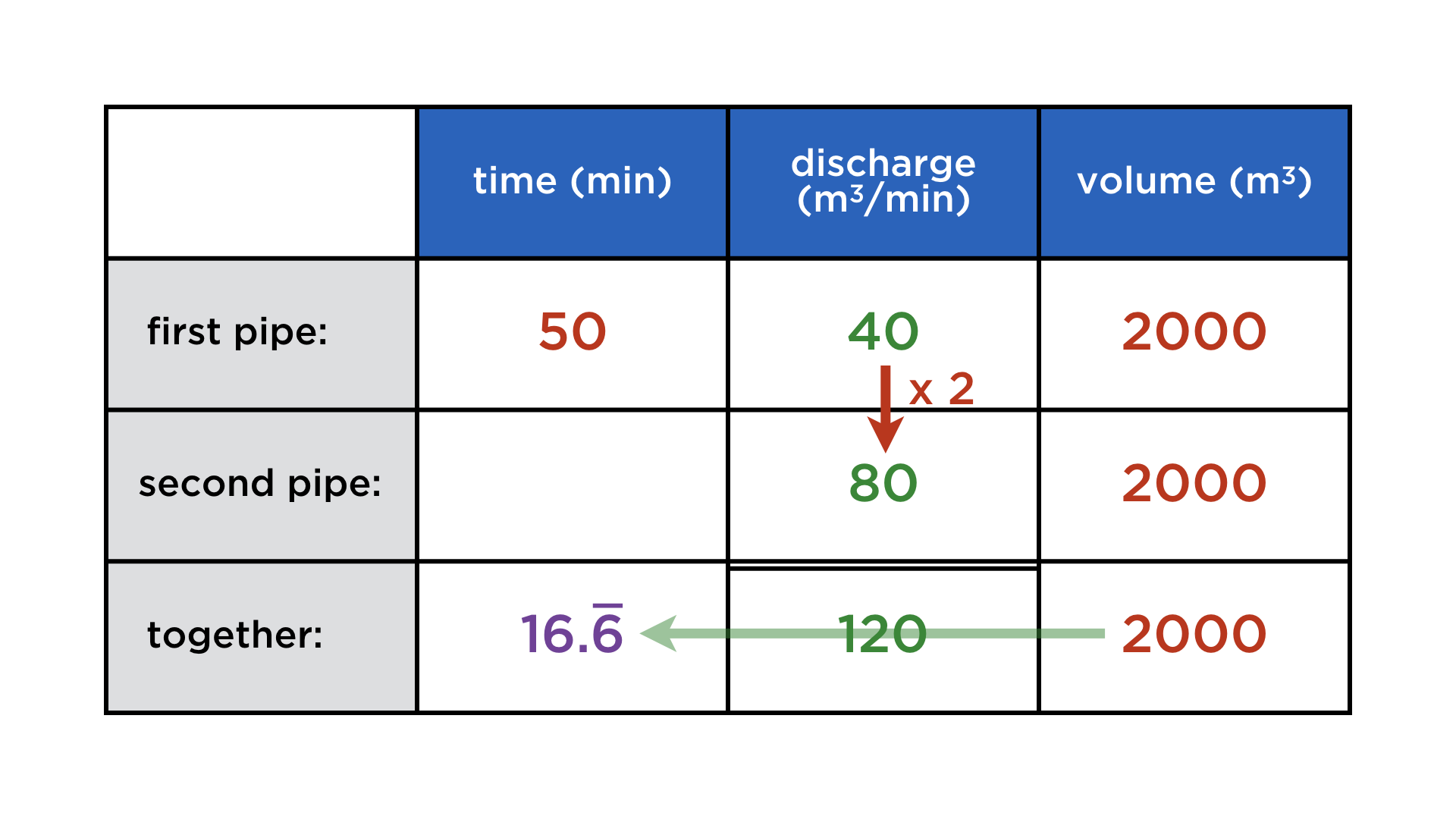
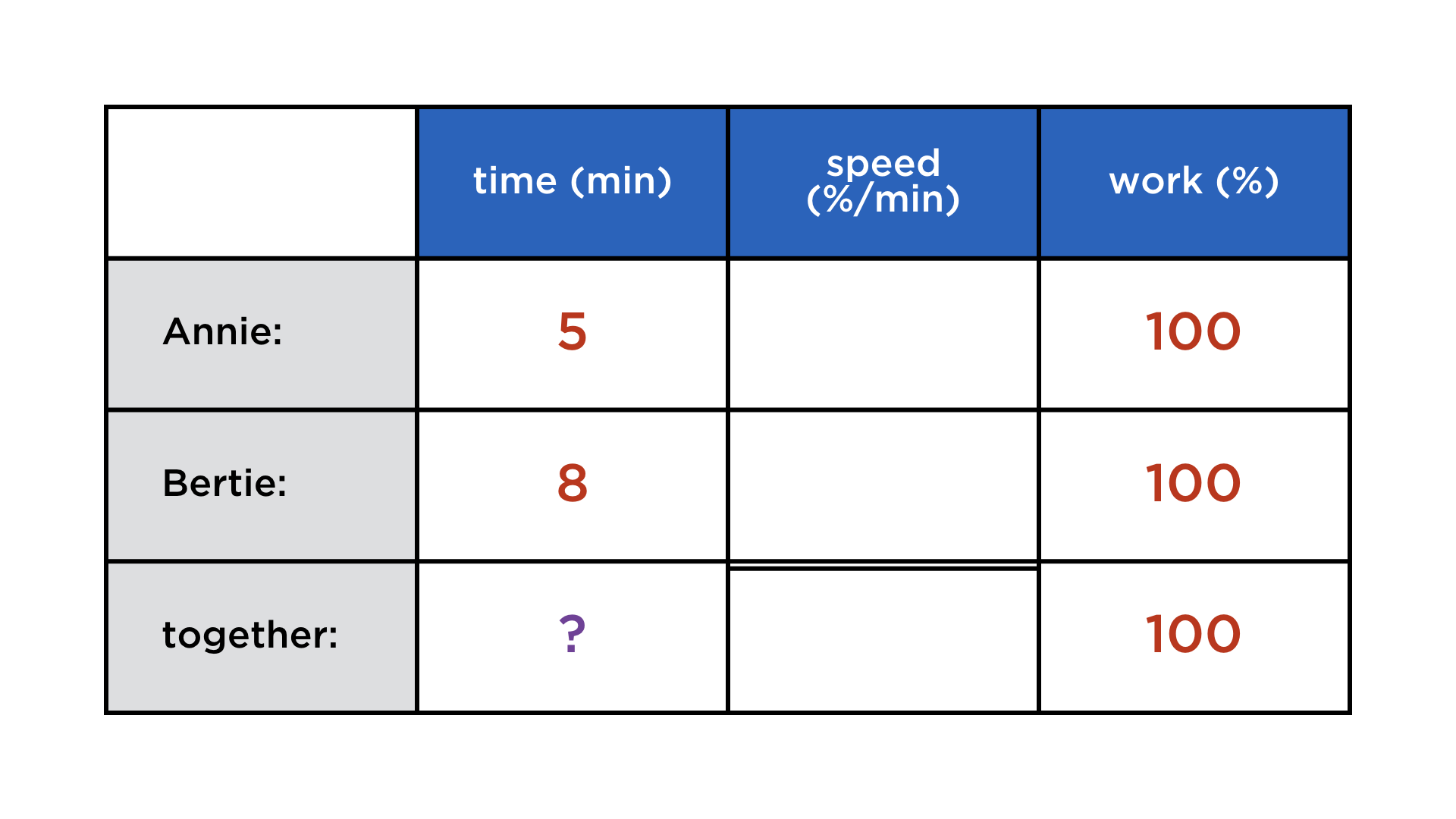
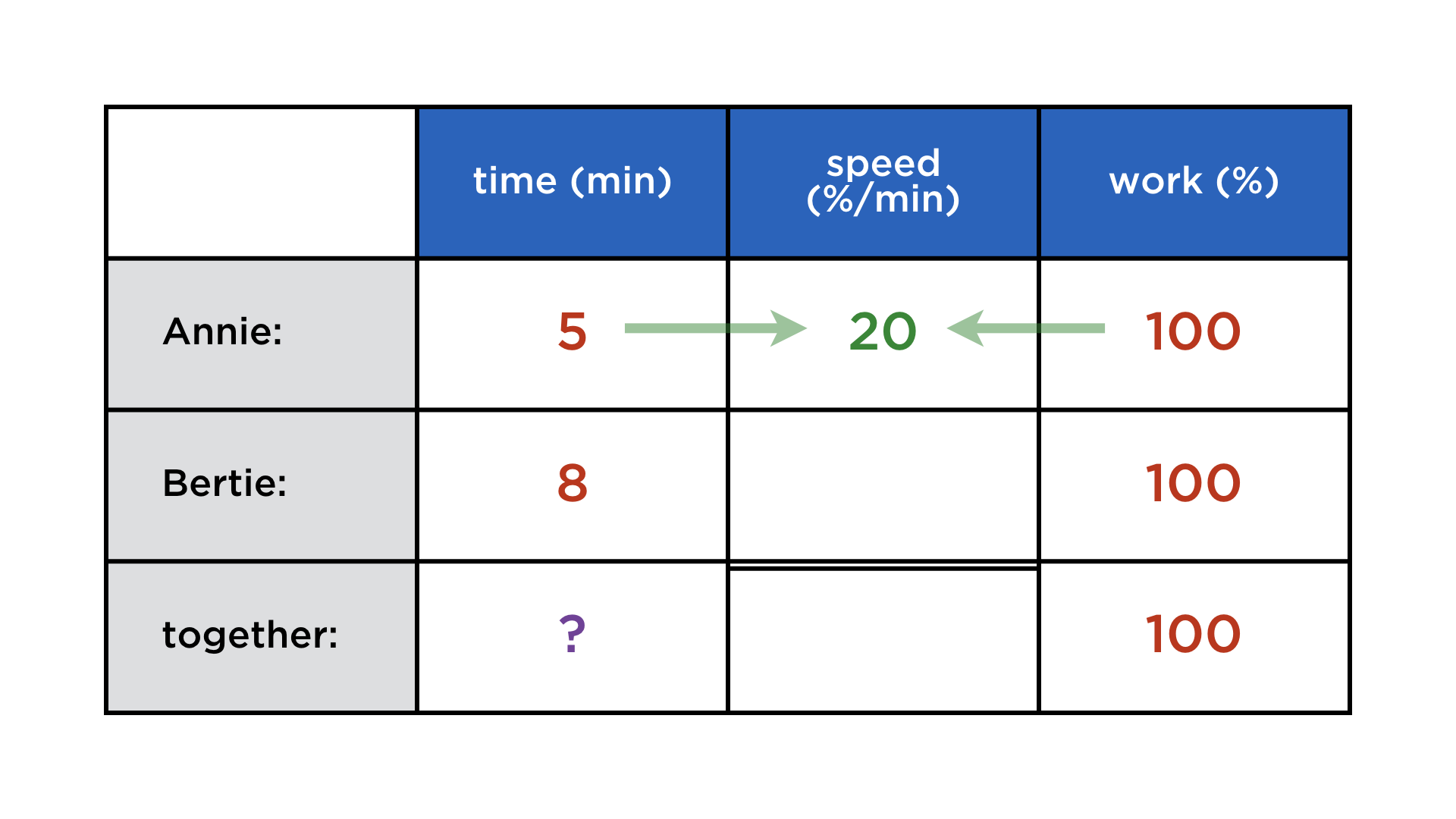
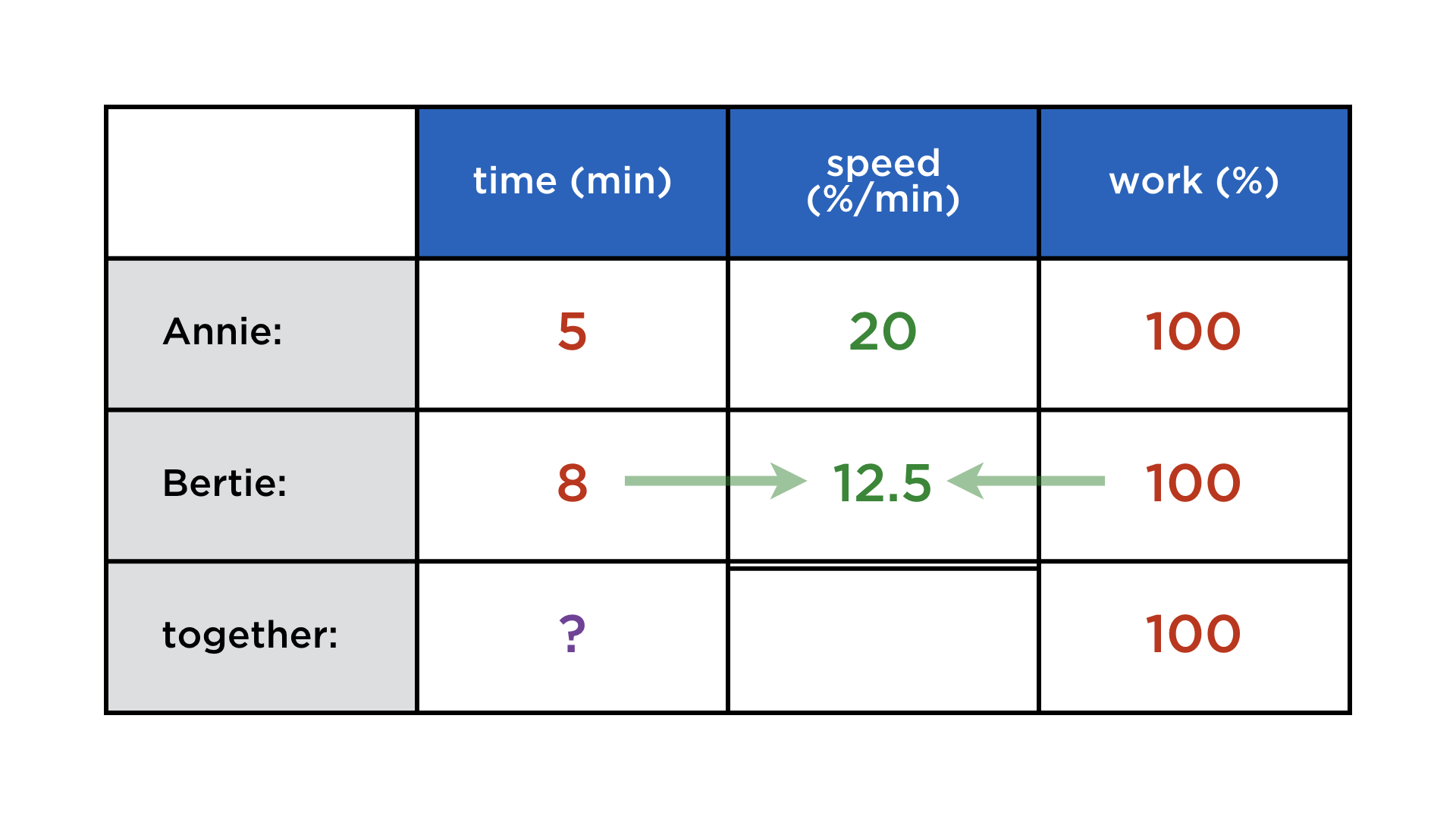
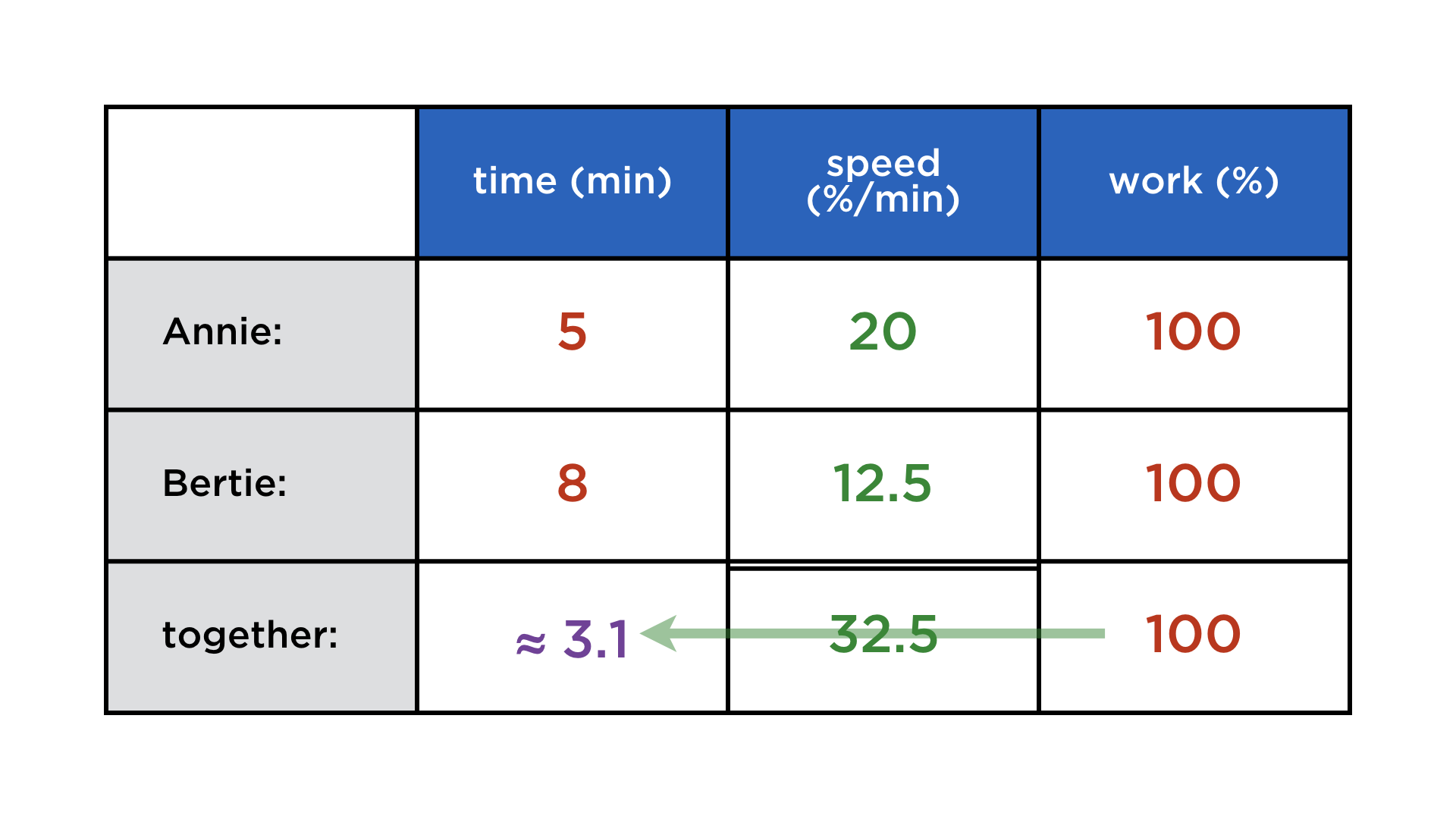
Mathematics and computers have a very paradoxical relationship, best expressed by juxtaposing these two images:

One the one hand, mathematicians co-invented the computer, and powerful numerical algorithms churn in the background to deliver us stunning graphics and other wonders. On the other, current user interfaces do not lend themselves easily to mathematical thought. Not only professional mathematicians cherish paper and blackboard, but also math teachers and their students. There is something so immediate about drawing and writing with your hands that is a requisite for creatively exploring math, but at the same time very hard to achieve on a digital device.

Digital math content: a parade of uncreativeness

Whenever mathematical content is digital (and not abstracted away into compiled code), it takes various forms, none of which resemble its haptic incarnation:

• Typeset expressions: They are created using either a markup language (LaTeX or MathML) or a „point-and-click“ formula editor. This is for publishing math, not exploratory calculations, because these interfaces add too much cognitive overhead.

• Code: Programming can be a vital part of exploring a mathematical problem, but for most people that do maths (whether voluntary or not), it is not the first reflex, because it involves learning a whole second formalism on top of the „paper version“.

• Prerendered content in quizzes, games etc.: This is what many have in mind when talking about „eduapps“, „e-learning“ etc. Fully committed to the answer-getting methodology of math education, it is as far from creative and exploring mathematical thought as you can get. Ironically, the users are not expected to work on the problems on the device itself, but whip out the still far superior pen and paper. Whatever added value the digital medium brings is restricted to the administrative layer.

• Educational videos: Most of those are of the tried-and-tested form of statically filmed chalk-and-talk. Again, the digital form adds nothing to the mathematical content, as most presenters are comfortably accustomed to doing maths by hand (and rightfully so).

Let’s have a chat

Yet with many students, I have seen the desire for creative mathematical expression using their most personal of tools. The tool they use to talk with their peers, to organize, collaborate, create, document, and share. Group chats across the world are buzzing with mutual homework help. And It works well for most subjects: the language-centered ones such as literature, history, civics; but also the artistic subjects, since images, audio and video can now as easily be created and shared as text.

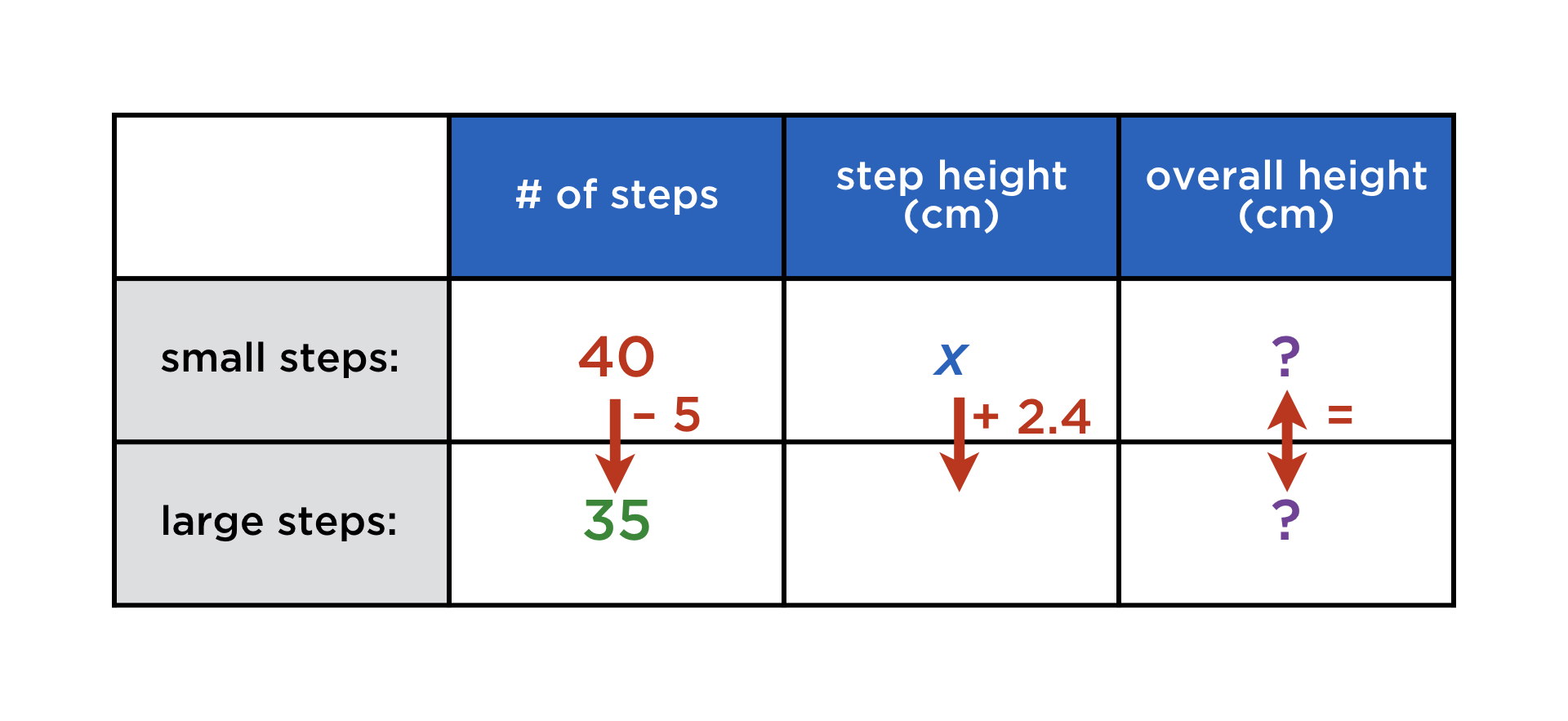
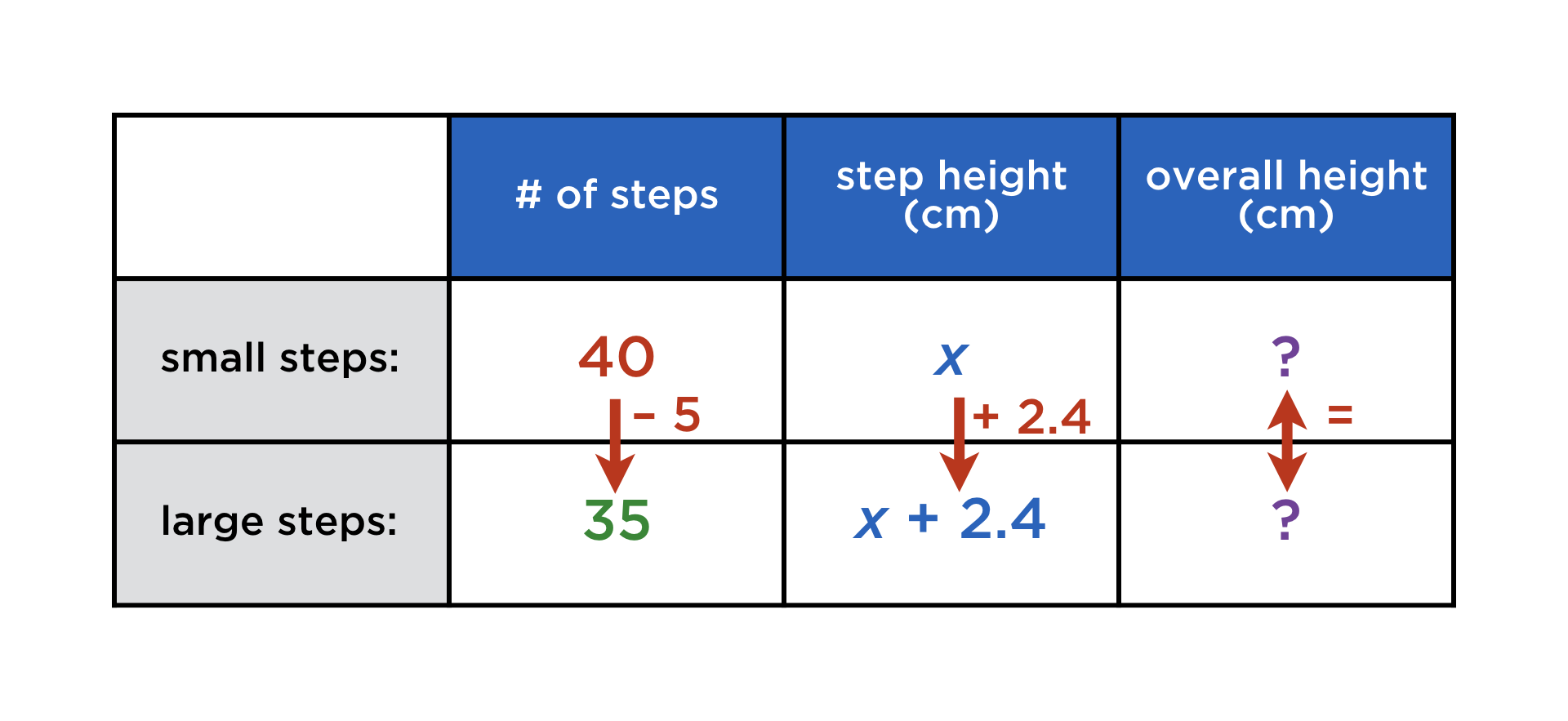
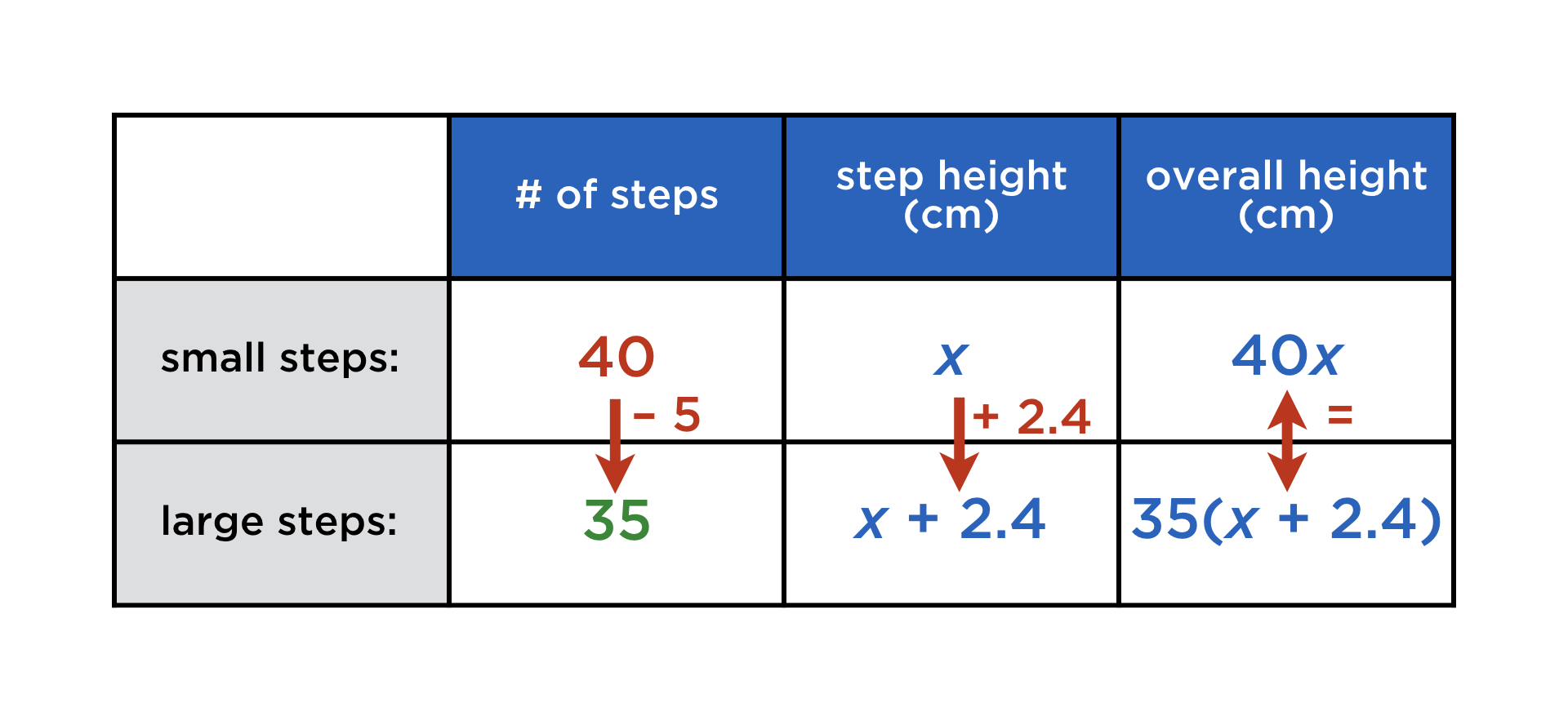
But there is one subject sticking out like a sore thumb: maths. Its content does not fit into linear text, however many new emoji get introduced. To this day, learners of maths have to awkwardly type their expressions in some sort of pseudocode (see picture above), or dig out pen and paper, then take a photo. You may think of this as a minor nuisance, especially if your own school days are long gone. But in any case it is a telling symptom of the second-class status that maths still has in the digital realm.

Plug time!

This is why I have created Formalize, a keyboard extension for iOS that lets you type math anywhere, in any app. Unlike most other purported „math keyboards“, Formalize is not just a palette of a handful of badly rendered Unicode symbols. It uses professional typesetting and outputs high-resolution images that you can share with anyone, so you can convey exactly what you mean in the form it deserves.

Formalize: only 3.99 USD / 4.49 EUR

Formalize Light (just TeX export): Free

Talk: Open play, not gamification!

I gave a short talk at the STEAM HUB Innovation Forum in Berlin (Oct 18-19), outlining what a truly open explorable medium for mathematics could look like.

Content Link Block

Select a page and create a visual link to it. Learn more

Blog

New shores: Beyond video

Over the past few months, I have worked with two remarkably gifted individuals, Grant Sanderson and Sridhar Ramesh, on creating high-quality animated videos on mathematics for the YouTube channel 3Blue1Brown. It has been the experience of a lifetime, both expanding and strengthening my (often contrarian) views on math education. At the same time, it has taught me a lot of technical skills for creative expression in ways I would never have dared imagine in the past.

After three successful videos, this collaborative effort has recently come to an end, as Grant has decided to scale his channel back to a solo project. You can read about his reasons for this step on his Patreon. I wish him the best of luck for the future of the channel (which has just recently crossed 1M subscribers!). Its quality in both form and content has raised the bar for online educational content of any field.

What does the future hold for me now?

Over the past few years, it has become increasingly clear that video's role as a powerful new medium for education is firmly established, and is in the midst of replacing the traditional textbook as students' learning resource of choice. Looking at most textbooks, I say: good riddance. Well-made videos are so much more effective at conveying certain sorts of content than the written word. Even though of course, they can never replace the genuine human connection with a caring teacher, educational videos are here to stay.

But in recent months, and already when I had just started producing 3Blue1Brown videos, I've become increasingly conscious of the medium's limitations. Explanatory videos climb only two of the three rungs on (what I like to call) the Ladder of Engaging Content:

1. Make it visual.
2. Make it dynamic.
3. Make it interactive.

Don't you kind of want to touch the mathematical objects in 3Blue1Brown's videos, reach into the screen? Play with them yourself, create your own? Then you are yearning for what Michael Nielsen calls an explorable medium for mathematics.

The idea is not new, in fact, parts of it can be traced back to the dawn of graphical user interfaces themselves. My own interest is fueled mainly by the mixture of delight and frustration that both GeoGebra and Desmos – in different ways – instill in me. Both apps illustrate a trade-off that appears to exist between power and usability.

As GeoGebra became more powerful over the years, its ease-of-use has greatly suffered. Many of my students had felt overwhelmed by the visual complexity of the early-2000s interface. (Truth be told, GeoGebra's latest versions have started to declutter the UI.)

Desmos, on the other hand, was designed from Day One for users of the mobile age. No menus, no tooltips, no tiny icons. Just touch your function! To keep that feeling of immediacy, the Desmos team treads very lightly when adding features. The price for this is that Desmos remains a graphical calculator – no less, but also no more. And still, it gives many of its users so much delight that their creative spark pushes against its boundaries!

The trade-off between power and usability seems to be unsurmountable. And yet, in recent years, a number of voices have started to question that premise. Ken Perlin's ChalkTalk and Michael Nielsen's Magic Paper are prototypes pointing in the right direction, as is this talk by ever far-out Bret Victor. Is the trade-off really a law of nature, or merely a self-fulfilling prophecy? Apps such as GeoGebra and Desmos have, each in their times, redefined what people believed possible in math-ed software. Who says we can't make that happen again?

Similarities with this are absolutely intentional.

Workshop on Visual Algebra

Back in March I held a workshop on Visual Algebra at a teacher's conference in Munich (109. MNU-Bundeskongress). I finally got around to posting the materials here.

It was exhilarating to meet some familiar faces, from former meetings and from Twitter, and a lot of new ones!

What video can and can't do for education

At the start of this year, I left the classroom to work full-time for the YouTube channel 3Blue1Brown. No introduction necessary to those who read this blog, I presume.

Why would I eschew a well-paying teacher position in Switzerland to go work at a scrappy start-up? Isn't "I wanna be a YouTuber" the new "I'll become a rapper anyway"? 

Here I expose my reasons for joining 3Blue1Brown. In a follow-up post, I will explain why working full-time in the classroom, as much as I enjoy it, is incompatible with the contributions to math education I hope to achieve.

In its self-description, 3Blue1Brown creates "animated math" – also in the original sense of the word of bringing life to something. Its videos are the best conveyors of what mathematical objects look like before the "mental eye" I have ever seen. No static image, not to mention a written text or string of symbols, comes close to its visual and dynamic immediacy. The videos show, don't tell, what a textbook can't or just won't.

Essence of Calculus, Chapter 4

Another aspect I have always admired is Grant's quest for visual interpretations where most others would simply shrug and say "It's just a formula, shut up and calculate." If only as a mental exercise, I have found such a self-imposed challenge extremely helpful for gaining insight into both the mathematical content itself and how to teach it. I owe this dedication to the iconic mode of thought to the eye-opening work of James Tanton.

A good picture can not only illustrate a formula or theorem, but even bypass whole calculations. Many page-filling textbook proofs could be supplanted entirely by a single well-crafted picture or animation. Granted, formal symbolic proofs and calculations bring the unmatched precision and expressiveness one needs to e. g. design a matching computer program. However they lack the clarity, accessibility and humaneness of pictures. The art of visual thinking has been sidelined in favor of symbolic manipulations ever since the invention of the printing press, followed by the various formalist schools and the advent of programming languages. As much as these developments have helped advance humanity technologically, they have also widened whatever gap there already was between the math "haves" and "have-nots" into a gaping canyon. It has catalysed similar divides throughout related fields. But the times of innocence when we could bask ourselves in the "Cult of the Expert" are long gone. This is an unsustainable situation, and the resentment it creates can be seen daily in the news.

Ok, back to math now.

If you look around on YouTube for educational math videos, most of them are just a person in front of a board, doing the age-old "chalk and talk". This is old wine in new wineskins. 3Blue1Brown is one of very few channels that actually harness the new capabilities of the new medium. Sure, other channels have flashy transitions and effects, cute cartoon characters and upbeat presenters, but the content proper is still mostly static and symbolic – glorified textbooks.

But well-crafted exposition videos can do a much better job at conveying mathematical understanding than textbooks. Far from me to claim they could ever replace the human connection that only a teacher in flesh and blood can provide. After all, teaching is so much more than just explaining. Still, the prevalent ways of explaining alone are in dire need for improvement.

Essence of Linear Algebra, Chapter 5

Despire the (warranted) calls for differentiation and personalized learning, I think there is a case to be made that some explanations are objectively better than others. The multitude of good teaching practices and learning situations, not to mention the spectacular failure of New Math, have dampened our expectations of finding the One True Way of teaching any particular concept. And while that is a sane position, such a culture of “Anything goes” (content-wise) can keep us from seeing the potential for genuine and substantial progress in rethinking content and overcoming historical baggage.

What was perhaps most striking to me when I stumbled upon 3Blue1Brown is the fact that Grant has no formal teacher training, “only” tutoring experience. Yet he has managed to internalize many  valuable skills and practices that many accredited teachers lack. They took me a long time to figure out as well, if only because they are not (cannot be?) taught in teacher training to any meaningful extent. Things such as an acute sense of visual design, cognitive load, and simple yet precise language. How to tell a compelling story, how to use subtle visual cues such as color and positioning to convey meaning nonverbally. How to recognize and question perpetuated traditions and hidden assumptions. Such talent is sorely lacking in our culture of communication, and especially in education.

Videos in the style of 3Blue1Brown are a big first step in the right direction. This is the reason why I took the opportunity to do everything I can to help expand its library, and develop whatever form its content may take in the future. If you are curious what next steps I think should follow in the world of math education, take a look at the visionary works of Bret Victor and Keith Devlin.

Reviving the Art of Storytelling

Recently, I have come across the new podcast "Ben, Ben & Blue". It covers "education, technology, and whatever else comes to mind." The second episode was dedicated to the question: Why do we still lecture? Manifold research has shown it to be an inferior mode of teaching, yet many educators do not resist the gravitational pull of this default option.

One main reason certainly is that lecturing is easiest to prepare and to plan. You sit down with a blank piece of paper, and think through a familiar problem or topic.  The result, after cleanup, will be a linear progression of ideas, to be cast into a lecture or book. It is the natural result of an individual's mental work, and this is precisely what makes it so treacherous.

The problem is the cleanup. All the messy, nonlinear inner dialogue gets discarded, the dead ends, doubts and invalidated counterarguments. Students are expected to travel a single paved road to final insight, but learning a topic means getting familiar with a whole landscape around it. This is what open forms of learning aspire to provide. But that requires anticipating student answers and counter-answers, typical and nontypical mistakes, alternative approaches – in short, a much broader and denser understanding of the logical structure underlying the topic at hand.

The lecture is, so to speak, only halfway to a great and effective lesson. In order to reach it, the cleaned-up material needs to be enriched again, not only with examples, illustrations, and the like, but also with meaningful student participation.

The Stories We Tell Ourselves

These ideas are not new, but much older than you might think. Thousands of years, in fact. Our current one-way method of lecturing is a remnant of the art of storytelling, which is as old as humanity itself. And good storytelling is interactive in all sorts of ways.

Ever since language began, huddled around a fire, we have hung on the lips of great storytellers. The first art, cave paintings and figurines, may have been used to accompany tellings and retellings of great stories. It is also one of children's first skills: to follow a story and to engage in it, and to tell their own. Take a look at these kindergardeners during storytime:

This is called "interactive read-aloud". The teacher engages the children by asking questions, providing time for reflection and discussion (also among the children), commenting on the story and pictures and even integrating physical activity. All of that in the span of six minutes!

These children are truly engaged in the story and will remember it thoroughly.

We memorize facts, but we remember stories. This is the magic our brains are hard-wired for. Stories contain characters, motivations, goals, interests, conflict, destiny, identity, rebellion, friends and foes, challenges, luck and misfortune – the whole gamut of the human condition. Stories make us notice and wonder. We revere our greatest storytellers, be that writers, comic artists or film directors. The most famous among scientists are also science's great storytellers. We don't even mind if the same stories are being retold over and over again (think of the countless superhero movie reboots), because great stories go far deeper than their plot. There is an iceberg of meaning, subtext, symbolism and interpretation beneath the surface. Novels and movies, while at first sight passive media, are accompanied by active engagement in the discourse and communities that form around them: critics, adaptations, magazines, fanfic, conventions, …

There is a hunger for great storytelling not only in literature and popular culture, but in science as well. Master storytellers such as Richard Dawkins and Neil DeGrasse Tyson make auditoriums burst at their seams. On YouTube, "edutainment" channels are among the most successful, because they show science and history in a way that school usually does not: as engaging stories.

Manas

The greatest stories of our time are the seed for entire subcultures. Again, this is not a new phenomenon: virtually every people in the world has some foundational myth, i. e. a story, and reveres those who can tell it most artfully. Just to name one example, the Kyrgyz people of Central Asia take great pride in the adventures of their mythical national hero, Manas. The Manas epic is twenty times as long as Homer's Iliad and Odyssey combined, yet it has been transmitted in purely oral form over generations of Manaschi, the master storytellers among the Kyrgyz:

Even today, Manaschi perform ritual recitations on special occasions such as weddings. History's great Manaschi are honored with busts:

Source: own work

Manas' purported burial grounds are a popular travelling destination:

Source: Wikipedia

and a giant statue of Manas watches over the capital's central square and national museum:

Source: own work

Even the international airport is named Manas!

This example goes to show what power stories have on us. Wh do we harness that power so little in our classrooms?

Lecturing as Storytelling

The classic lecture (or teacher-centered instruction in classrooms) is but a faint shadow of the ancient art of storytelling, all the elements that make it engaging and humane are stripped away for reasons of time, effort and money. It is cargo-cult teaching. Some students are good with lectures, they have enough experience, background knowledge and imagination to fill in what the lecture lacks. This is in fact a trained skill: the ability to follow longer and longer stories, i. e. to internalize one's engagement. The benefit of this valuable ability lies in access to deeper stories, e. g. novels.

A good teacher provides and moderates a level of engagement appropriate to the developmental level of their students. In this regard I have the utmost respect for kindergarden and grade school teachers! In higher education, however, we tend to overestimate our students' abilities for internal engagement, and underestimate the benefits of interactive storytelling. "That's for children, not grownups!"

Let us revive the art of storytelling in education. Behind every formula there lies a story, complete with exposition, conflict and resolution. Tell the history of your subject, full of dead ends and surprises. Make your students tell their own part in the grander story: comments, retellings, variations or sequels. Then your class will take part in the most human of traditions – and your students will remember it for a long time to come.

New video series: Visual Algebra

Algebraic notation is broken.

By that I mean that it is a major hurdle for many who struggle with mathematics, a major source of typical mistakes, and still way less consistent than we teachers would care to admit. It has features such as:

• invisible brackets: $x+y\cdot z$, $\frac{a+b}a$
• ambiguous use of brackets: $a(b+c)$ vs. $f(x+1)$
• function notation without brackets: $\sin\, x$
• triple meaning of the equal sign (equation, identity, definition)
• right-to-left function notation: $g\circ f(x)$

These examples may seem trivial to anyone already fluent in algebra, but they can be real stumbling blocks for novices. Worse yet, math tends to become more and more symbolic as school progresses, with drawings serving only as informal illustrations of the "actual" math. We are drowning students in notation. Huge swaths of exercises consist of purely symbolic calculations, such as simplifying fractional expressions, completely devoid of any geometric meaning.

(This follows the historical path, but something got lost on the way, as a price to be paid for the power of algebra. Symbolic notation was introduced to help grapple with geometric figures – the "actual" math back in the day –, but later it took center stage while relegating figures to the status of mere illustrations. What got lost – intuition – was scoffed at for being error-prone and misleading. This of course culminated in the formalist school of mathematics, where even proofs were considered a form of computation.)

But we are visual creatures. Even mathematicians find their ideas most often by doodling, before casting their thoughts into formulas. Geometric figures are intuitive, accessible, self-explanatory and friendly. Why have we cast aside the power of drawings, deemed "informal", in favor of dense, one-dimensional strings of (sometimes arcane) symbols? A good notation should make computations obvious, and mistakes almost impossible to make. In other words, it is intuitive. Any good programmer can tell you that. We need a better notation for algebra. Better than the historically grown amalgation that people mistake for the essence of algebra now. Something that brings intuition back to algebra.

Let's reclaim the power of visualization over computation.

I have therefore started a new video series called "Visual Algebra" ("Doodle Algebra" to its friends). It is a novel approach to school algebra using a more intuitive, graphical notation that can supplement the standard notation not only for deeper understanding, but also for more thoughtful manipulation.

Visual Algebra is not merely a collection of illustrations. It can be used to perform entire calculations completely within the visual representation! Not only that, but you can even mix and match it with the standard notation to selectively visualize only parts of an expression. Even fractional expressions find their most natural geometric meaning, and this in turn informs their simplification.

The full playlist in embedded below. I will add videos in the coming weeks, covering these topics:

• addition and subtraction
• multiplication and division
• fractions and fractional expressions
• powers and roots
• logarithms

The Quest for the Lost Quadrilateral

Recently, David Griswold posted this in #geomchat:

Hey #geomchat - what am I missing in my complete inclusive quadrilateral hierarchy? "At least one pair of consecutive = sides?" Has name? pic.twitter.com/XFlP5fds9u

— David Griswold (@DavidGriswoldHH) July 21, 2017

I was immediately struck by the diagram's asymmetry – even though it contains all standard types of convex quadrilaterals. As if a line connecting trapezoid and kites were missing, which of course cannot be. So what else is?

The apparent skewness of the classification is especially insulting given the beautiful symmetry in its lower part, where rectangles and rhombuses exhibit a deep duality between lengths and angles. Let's revel in it for a brief moment before we tackle the larger picture.

Classifying parallelograms

A parallelogram, as you might recall, is this kind of quadrilateral:

All four properties are logically equivalent, meaning that either of them can be taken as the defining property, and the others derived from it. (Personally, I prefer the first one – nomen est omen.)

Rectangles are a special class of parallelograms:

The angles at the vertices are not only pairwise equal, but as all four as well (and thus all are 90°). It follows that the diagonals, in addition to still meeting in their common midpoint, have equal length. This last property is often not explicitly mentioned in geometry class, but implicitly used in application problems. Again, one could go the other way around and use the diagonal property as the definition and derive (how?) the right-angle property.

Another special class of parallelograms are the rhombuses:

In a rhombus, all four sides have the same length, not only as opposite pairs. A consequence of this is that the diagonals meet at a right angle (think congruence). There is also the noteworthy property that the diagonals bisect the angles, which we will get back to shortly.  Finally, the classes of rectangles and rhombuses intersect to form the class of squares.

Have you noticed something peculiar? Because I have.

As @JamesTanton likes to put it: "Whoa."

Take it in slowly. Revel in it. This is, hands down, one of my favourite chapters in geometry.

Compare the rectangle and rhombus for a while longer. Notice how any symmetry of lengths in one mirrors a corresponding symmetry of angles in the other?

Now, why would such a piece of exquisite beauty sit right next to a helter-skelter classification of the other quadrilaterals? This would be unbearingly insulting to the mathematician's mind. Hence I sought out to find the missing piece, letting the duality between lengths and angles be my guide.

Extending the duality

Look at the kite. It shares some commonality with the rhombus, in that the diagonals meet at right angles, but only one bisects the other. In addition, one of the diagonals acts as a bisector of a pair of opposite angles, whereas in the rhombus both diagonals do.

Now look at the trapezoid and its special case, the isosceles trapezoid. Regarding their diagonals and angular bisectors, not much of interest is going on. But bear in mind the duality between angles and lengths, or rather sides. What is there of notice about a trapezoid's sides?

• In a trapezoid, a pair of opposite sides is parallel. Put differently, their segment bisectors are parallel:

• In an isosceles trapezoid, these opposite segment bisectors coincide:

Let's rephrase the property of the isosceles trapezoid and compare it with the kite:

• In an isosceles trapezoid, a pair of opposite sides shares a common bisector. (It follows that they are parallel.)
• In a kite, a pair of opposite angles shares a common bisector.

The isosceles trapezoid generalizes to the trapezoid by demanding that the side bisectors be only parallel (and hence the sides themselves are parallel). This suggests a corresponding generalization of the kite, which I christen a "kitoid":

Definition. A kitoid is a convex quadrilateral in which a pair of opposite angles has parallel angular bisectors.

(The outer point serves as a "handle" to manipulate the kitoid's form.)

Then we can arrange kitoids, kites, trapezoids and isosceles trapezoids in a nifty little 2x2 diagram:

I move we call the clunkily named "isosceles trapezoid" simply "trapeze" for symmetry. (My fellow German speakers might disagree, because "Trapez" already stands for "trapezoid", but I say we take a hit for the team.)

You can easily check the following statements which embed kitoids into the greater hierarchy:

Theorem.
(a) The kitoids that are trapezoids are precisely the parallelograms.
(b) The kitoids that are trapezes are precisely the rectangles.
(c) The kites that are trapezoids are precisely the rhombuses.
(d) The kites that are trapezes are precisely the squares.

The classification of convex quadrilaterals is now breathtakingly symmetric:

(Red arrows indicate restricting definitions, black arrows intersections.)

What about area?

There is a useful expression for the area of any trapezoid, trapeze or not:

However, the area formula for kites:

appears to resist easy generalization to kitoids, because of a lack of right angles. Unlike a kite, a kitoid cannot be easily doubled into a rectangle. Two possible generalizations of the kite doubling are a doubling into a parallelogram:

and one into a "rectangular ring":

(The inner rectangle has to be subtracted because of overcounting, as a consequence, the area difference between the rectangles is twice the kitoid's area.)

On the other hand, the standard constructions that accompaniy the area formula for trapezoids, such as the one above, have no obvious analogue for kitoids. It might be too much to ask for a simpler generalization of a kite's area to a kitoid. Unless the property that corresponds to the trapezoid area, under the duality between angles and sidelengths, is something different altogether.

What about concave and complex quadrilaterals?

Yes what about them? How far does the angle-side duality permeate the hierarchy of quadrilaterals? I have no idea for now. Things might get pretty messy, pretty fast. Or they might turn out to exhibit otherworldly beauty. You never know when it comes to these fantastic beasts we call quadrilaterals.

A (somewhat) simple proof that π is irrational

I have made a video series on Lambert's proof of the irrationality of π. Enjoy!

YouTube link

Contaminated angles

Have you heard of the wine-water mixing puzzle? (Spoiler alert: solution is given right after it)

Two pitchers contain equal amounts of different liquids (wine and water, for example). A glassful from the water pitcher is poured and mixed into the wine, and then a glassful from the now diluted wine is poured back into the water. Which pitcher is now more contaminated, i. e. contains more of the other liquid?

Before you whip out a pen and the back of an envelope, or throw your arms up in the air, here is the surprising answer: both are equally contaminated! One can reason algebraically (as on Wikipedia) or simply notice that whatever amount of wine is ultimately in the water must have displaced an equal amount of water into the wine, if both pitchers are back to their initial volume.

Astonishingly, this has a very nice geometric picture in terms of two straight angles "contaminating each other":

Through the rotation, some of liquid 1 (wine) lands in the half-plane of pitcher 2 and vice versa. The respective amounts are represented by angles, which by the vertical angle theorem must be equal.

The pitchers even do not have to have the same volume, as long as each ends up with its initial volume:

Don't you just wish math had more of these simple, intuitive, eye-opening picture moments? Save that wish, because it does!

(Careful though: the amounts exchanged, as represented by the opposing acute angles, are not the amounts of liquid poured, which are slightly larger. After pouring water into wine and mixing, some of that water is transferred back into its original pitcher. The intermediate stage, as well as the process of mixing, do not have an easy geometric picture as far as I can see. But what ultimately matters in the puzzle is only the final state in comparison to the beginning.)

Thanks to Dr James Tanton (@jamestanton) who gave me the idea while I was watching his remarkable lecture series "The Power of Mathematical Visualization" on The Great Courses Plus. It should be required coursework for any beginning math teacher!

Getting to the root

Last time, we have established the existence of irrational numbers without any mention of square roots. Why now is e. g. $\sqrt{2}$ among them? The standard proof overuses variables and cannot be easily generalized. Here I present an purely arithmetical proof that establishes a simple condition for the irrationality of any root of any rational (i. e. of the form $\sqrt[n]{\frac pq}$, $p,q,n\in\mathbb N$).

The overarching idea is to work through a fair selection of arithmetical examples until the general method (in this case: of finding a square root) becomes visible. Then, present examples for which the method obviously fails, and a general criterion can be found by comparing and contrasting the examples' essential and contiguous elements. A good selection of arithmetical examples exhausts all thinkable possibilities and can thus serve as basis for a discussion of the general case. Such a proof "by prototyping" may lack in rigor and formality, but gains in clarity and constructiveness.

Easing in

Let's start by finding the root of a few square numbers:

$\sqrt{49}=\sqrt{7^2}=7, \sqrt{121}=\sqrt{11^2}=11, \sqrt{81}=\sqrt{9^2}=9.$

Easy enough. What about larger numbers, e. g. $\sqrt{196}$? We decompose it into prime factors and identify double factors:

$196 = 2\times 2\times 7\times 7 = (2\times 7)\times (2\times 7)=14\times 14=14^2 \Longrightarrow \sqrt{196}=\sqrt{14^2}=14.$

We can even flex our muscles with the laws of exponents:

$576 = 2^6\times 3^2 = (2^3\times 3)^2 \Longrightarrow \sqrt{576}=2^3\times 3 = 24$

$\sqrt{5625}=\sqrt{3^2\times 5^4}=\sqrt{(3\times 5^2)^2}=3\times 5^2=75$

$\sqrt{9801}=\sqrt{3^4\times 11^2}=3^2\times 11=99.$

These three examples show (in varying notation) the general method:

• decompose the radicand into prime factors
• pair up the factors (i. e. write the product as a square)
• collect the single prime factors into the result.

The sky's the limit:

The factors don't necessarily have to be prime, as long as they can be paired without leftovers:

$\sqrt{10^{100}}=\sqrt{(10^{50})^2}=10^{50}.$

Sure, but…

All this is fine and dandy as long as the radicand has been specially prepared by the teacher. What about:

$\sqrt{99}=\sqrt{3^2\times 11}$?

The prime factorization tells us the ugly truth: the radicand is not a square number, so the root cannot possibly be an integer. Our calculator confirms this, but can only spew out decimal digits, not an exact value. At this point, the best we can do is partial reduction: extracting whatever double factors there are and keeping the leftovers under the root:

$\sqrt{3^2\times 11}=\sqrt{3^2}\times \sqrt{11}=3\sqrt{11}.$

The root is now at least "simpler", but an exact value is still lacking. At least we have reduced the problem to a "smaller" (yet still infinite) class of square roots. Once we know what $\sqrt{11}$ is, we also have a value for $\sqrt{99}$.

in any case, we can formulate the condition for the factor method to succeed as a theorem:

Theorem. The square root of a positive integer $N$ is itself an integer precisely when all prime factors of $N$ occur in pairs.
Proof. The square $R^2$ of any positive integer $R$ contains every prime factor of $R$ twice (counted with their multiplicities). An integer $N$ with an unpaired prime factor thus cannot be the square of some integer $R$.

Hope springs Rational

What does it mean to "know" what $\sqrt{11}$ "is"? Bear in mind that for a student who first encounters the root symbol, $\sqrt{11}$ is not simply a number but a problem awaiting an answer in decimal or fractional notation. Make sure your students view fractions as an equally valid, if not better representation than decimals. Then the shortcomings of the calculator answer become apparent. In order to strengthen this motivation, you can ask calculator-clingy students to e. g.:

• check the numerical result by squaring: a cheap model will return $1.41421356^2\simeq 1.99999999$
• calculate $\sqrt{1000000001}\simeq 10000.00005$: here the available significant digits are taken up by zeroes, and the "interesting" tail is rounded off

In any case, whether by persuasion or habit, instill in your students the aim to find an exact rational answer for the square roots that don't resolve to an integer.

Rational Radicands

This might seem to be the perfect moment to present a proof that e. g. $\sqrt{2}$ is irrational. I recommend that you resist this urge, and instead turn your students' attention to extending the factor method to rational radicands, leaving the problem of unresolved integer radicands for now. Let them work out:

$\sqrt{\frac{16}{25}} = ?$

$\sqrt{\frac{289}{81}} = ?$

$\sqrt{\frac{125}{245}} = ?$

$\sqrt{0.0625} = ?$

These examples illustrate that the factor method works just as well for fractions (some reducing and expanding may apply). Once the numerator and denominator are both written as products of paired factors, the root can be resolved:

The denominator and numerator decompose separately, and therefore we can extend the condition for integers:

Theorem. The square root of a positive rational $\frac pq$ (reduced form) is itself a rational precisely when all prime factors of $p$ occur in pairs, and the same condition for $q$.
Proof. The square $(\frac nm)^2$ of any positive rational $\frac nm$ contains every prime factor of $\frac nm$ twice (counted with their multiplicities). An integer $\frac pq$ with an unpaired prime factor in $p$ or $q$ thus cannot be the square of some rational $\frac nm$.

This now answers the open question of the unresolved square roots:

Corollary. The roots of the non-square integers (i. e. all naturals except 0, 1, 4, 9, 16, …) are all irrational. Therefore $\sqrt{2}\simeq 1.4142135623\dots$ $\sqrt{3}\simeq 1.7320508075\dots$ $\sqrt{5}\simeq 2.236067977\dots$ $\sqrt{6}\simeq 2.4494897427\dots$ etc. are all infinitely long decimals that never repeat.

This formulation is much more general than the usual restricted result $\sqrt 2\notin\mathbb Q$ (and maybe, as an exercise, $\sqrt 3\notin\mathbb Q$), and still just a special case of the preceding theorem. Yet both can be shown on arithmetical examples alone.

Higher-order Roots

Finally, the extension to cubic roots and general roots is straight-forward:

Theorem. The $n$-th root $\sqrt[n]{\frac pq}$ of a positive rational $\frac pq$ (in reduced form, $p,q,n\in\mathbb N$) is rational precisely if the prime factors of $p$ can be grouped into sets of $n$ identical factors each, with no factors left, and the same condition for $q$.

Concluding Remarks

The irrationality of roots is a topic where algebraic notation obscures more than it clarifies, and thus I deem the present, arithmetical approach more valuable for students. It is much closer to the operational day-by-day work, while still providing valid reasons for general theorems. In a later post, I will expand more generally on the benefits and possible critiques of this kind of proof "by prototypes".

The wondrous and mysterious rational numbers

In the last post, I argued how the classical proof of the existence of irrational numbers is didactically flawed on several accounts. Here I present my own, purely arithmetical, approach.

It all starts with a thorough appreciation of rational numbers. Before introducing real numbers, my students are well-trained in fraction arithmetic and the various accompanying geometric pictures. Of course they know about decimal numbers already, and are eager to type in any fraction to find the "true" value. Students have an almost unhealthy obsession with decimal numbers, as if it told you more, or even everything there is to know about a number. This is not so!

This blog post presents a way of transitioning from $\mathbb Q$ to $\mathbb R$ that aims to break the "decimal fixation" and to illustrate the "incompleteness" of the rationals in a purely arithmetical, less convoluted way than is usually done (see earlier post here).

TLDR

One of the goals here is to appreciate the distinction between a number and its representations. To "calculate" a fraction is to switch from the fractional to the decimal representation of the same number. Observing what kinds of decimals can occur is a very educational example of a classification theorem, perfectly accessible without the use of algebra or higher formal reasoning. Both the fractional and decimal representations have their advantages and drawbacks, and it is insightful (if not indispensable) to understand how one can switch from a decimal back to a fraction.

Against this backdrop, the existence of irrational numbers (decimals that cannot be rewritten as a fraction) might appear almost trivial. This important moment in any student's mathematical career lends itself to reflect critically a few "intuitions" we believe to have about numbers. (I will explore this in a later post.)

Fractions as decimals: let's go explore!

Remember how I mentioned students's love for their calculators? We can harness it in the beginning (its limitations will become visible soon enough). Here are a few examples of simple fractions as decimals:

$\frac 12 = 0.5$

$\frac 13 = 0.333333\ldots = 0.\overline{3}$

$\frac 23 = 0.666666\ldots = 0.\overline{6}$

$\frac 14 = 0.25$

$\frac 34 = 0.75$

$\frac 15 = 0.2$

$\frac 16 = 0.1666666\ldots = 0.1\overline{6}$

$\frac 17 = 0.14285714285714\ldots = 0.\overline{142857}$

$\frac 18=0.125$

$\frac 38 = 0.375$

$\frac 78 = 0.875$

$\frac 19 = 0.111111\ldots = 0.\overline{1}$

$\frac 29 = 0.222222\ldots = 0.\overline{2}$

$\frac 1{10} = 0.1$

$\frac 1{11} = 0.09090909\ldots = 0.\overline{09}$

$\frac 1{12} = 0.08333333\ldots = 0.08\overline{3}$

A few things can be observed:

• Some decimals are short and to the point.

• Others have an infinite number of digits (students like to say: "they are infinite"), in a repeating pattern.

• There can be a single digit that repeats, or a string of two or more digits repeating.

• The repeating pattern (period) does not always start right after the decimal point.

The long period of $\frac 17$ sticks out like a sore thumb. It has a few crazy cousins further along:

$\frac 1{13} = 0.\overline{076923}$

$\frac 1{17} = 0.\overline{0588235294117647}$

$\frac 1{19} = 0.\overline{052631578947368421}$

There are also the weird

$\frac 1{81} = 0.\overline{012345679}$

(sic!) and the mysterious

$$\frac 1{9801} = 0.0001020304050607080910111213\ldots$$

It is also worthwhile to notice this pattern (for later):

$$\frac 19 = 0.\overline{1}$$

$$\frac 1{99} = 0.\overline{01}$$

$$\frac 1{999} = 0.\overline{001}$$

$$\frac 1{9999} = 0.\overline{0001}$$

Making sense of all this

Is there any order behind this plethora of behaviors? Let's do the division by hand in a few select cases, such as these:

The third example shows where the periodic behavior comes from, by looking at the remainders at each step and noticing that the repetition kicks in the moment the remainder 20 appears again. Is it guaranteed that the remainders will eventually repeat? A strong hint at the answer, and its justification, lies in the long division of $\frac 17$:

These examples show two insights:

• The periodic repetition in the decimals stems from a repetition in the remainders.

• The remainders are bound to repeat eventually (or become 0), because they come from a finite pool of possible remainders (the positive integers less than the numerator).

Classifying

While our observations were on a small number of arithmetical examples only, the reasoning about the calculations, i. e. the sense we made of their behavior, is entirely general, independent from the chosen numbers. I claim that this is enough to constitute a proof of the following theorem:

Theorem. The decimal representation of a rational number $\frac pq$ ($p$, $q$ integers) is either:

• an integer,
• a terminating decimal, or
• a repeating decimal.

In particular, this tells us that the mysterious decimal representation of $\frac 1{9801}$, too, is bound to repeat eventually. (In fact, it repeats after having cycled through all possible pairs of digits, except for the second-to-last:

$$\frac 1{9801}=0.\overline{000102030405\dots9799}.)$$

Which representation is better?

Now comes the moment to address "decimal fixation" head-on. Why should we continue dealing with fractions when we now have decimals? The answer lies in comparing a few problems in either representation. Give the following "a" problems to one half of the class, and the "b" problems to the other, and have them work by hand:

Problem 1a. $\frac {26}{75}+\frac {77}{100}=?$

Problem 1b. $0.34\overline{6} + 0.77 = ?$

Problem 2a. $\frac{3}{8}\times\frac{4}{15} = ?$

Problem 2b. $0.375 \times 0.2\overline{6} = ?$

Problem 3a. Which is greater: $\frac{7}{11}$ or $\frac{13}{20}$?

Problem 3b. Which is greater: $0.\overline{63}$ or $0.65$?

By comparing the effort needed for each problem, it becomes apparent that the decimal representation is much better suited for adding and comparing, while multiplication is the strong suit of the fractional representation. This is why we math teachers insist on keeping the latter around (especially since multiplication is the most frequent operation in higher and applied math). So it turns out that the fractional representation can often give us more useful information about a number than its decimal representation, and vice versa.

Moonwalking back to fractions

At this point, one can already see what irrational numbers are about: they are decimals that fall in none of the three categories listed in the theorem. Or at least, such decimals certainly have no fractional representation. But is this the only restriction that applies? What about very complicated repeating decimals such as $0.987\overline{14916253649}$ or $0.\overline{1234567891011112\dots9989991000}$: do they also have a fractional representation? Or are they irrational?

While the existence of irrational numbers can already be deduced here, and the question of how to transition from a decimal to a fractional representation casts no doubt on this result, it is worth investigating to gain a thorough understanding of two deep concepts:

• Fractions and decimals are but two different representations: none is a truer form than the other. They both have their advantages and drawbacks. (This is why from now on we speak of rational numbers, rather than fractions.)

• Indeed, irrationals are precisely the decimals that fit none of the aforementioned three categories.

So how do we represent a decimal as a fraction? A terminating decimal is easy: it is always an integer multiple of one of the "base-ten" fractions

$$0.1 = \frac 1{10},\quad 0.01 = \frac 1{100},\quad 0.001 = \frac 1{1000}, \quad\ldots$$

so that e. g.

$$3.285 = 3285\times 0.001 = 3285\times\frac 1{1000} = \frac{3285}{1000} = \frac{657}{200}.$$

The "base-ten" fractions (inverse powers of ten) are the building blocks of the terminating decimals.

Repeating decimals require a bit more work. But we can find the general method by looking at select examples alone:

$$0.\overline{2} = 2\times 0.\overline{1}=\frac 29$$

$$0.\overline{35} = 35\times 0.\overline{01} = \frac{35}{99}$$

$$0.\overline{123} = 123\times 0.\overline{001} = \frac{123}{999} = \frac{41}{333}$$

The primitive fractions $\frac 19$, $\frac1 {99}$, $\frac1 {999}$, … turn out to be the building blocks of the purely repeating decimals, just as $\frac 1{10}$, $\frac1 {100}$, $\frac1 {1000}$, … were the building blocks of the terminating decimals.

What about periods that don't start right after the decimal point? Let's do the easier case of just zeroes before the period first:

$$0.0\overline{4} = 4\times 0.0\overline{1} = 4\times\frac{0.\overline{1}}{10} = 4\times \frac 1{10}\times\frac 1{9} = \frac 4{90} = \frac{2}{45}$$

$$0.00\overline{234} = 234\times\frac {0.\overline{001}}{100} = 234\times \frac 1{100}\times\frac 1{999} = \frac{26}{11100}$$

The inverse powers of ten help their friends find the right place after the decimal point!

Lastly, decimal numbers with non-zero digits before the period can be split into their non-repeating and purely repeating parts:

$$1.1\overline{45} =  1.1 + 45\times 0.0\overline{01} = \frac{11}{10} + \frac{45}{990} = \frac{63}{55}.$$

We have thus established, by exhaustion, the converse of the classification theorem from above:

Theorem. Any number that is either:

• an integer,
• a terminating decimal, or
• a repeating decimal
can be writte as the ratio $\frac pq$ of two integers $p$ and $q$.

What's missing?

Already in its first form, the classification theorem begs the question: what about decimals that fall in none of the three categories, in other words: that go on in some other fashion than a period? We can think of simple examples such as:

$$0.12345678910111212131415\ldots,$$

known as Champernowne's constant, or

$$0.101001000100001\ldots$$

or the Copeland-Erdös constant

$$0.23571113171923\ldots$$

(have students guess the pattern in that one!). So, what about such numbers? They simply cannot have a fractional representation, and we call them irrational numbers. Ta-da!

A bit anticlimactic, I know. But I seriously cannot see what the big fuss is about the existence of irrational numbers. Once you do math in a decimal system rather than relying on proportions between integers (looking at you, Ancient Greeks), this is a trivial result.

Where is the wonder?

As I hope to have demonstrated, there is plenty of wonder and mystery already in the rational numbers. Some things have even been left unmentioned:

• The always controversial $0.\overline{9} = 1$, with its various proofs.

• The resulting insight that decimals are not a unique representation, neither for terminating ($0.25 = 0.250 = 0.24\overline{9} = 0.25\overline{0}=\ldots$) nor repeating decimals ($0.\overline{12}=0.1\overline{21} = 0.\overline{1212}=\ldots$), a slight nuisance that also riddles the fractional representation: $\frac 23=\frac 46=\frac{66}{99}=\ldots$

• The fact that the rationals are dense on the number line (there is no "number right after 1").

• The geometric meaning of repeating decimals (self-similarity in nested intervals).

• Which fractions have a periodic decimal? Can we anticipate this before the long division?

• Same question for the length of the period.

• Positional representation in bases other than ten: In which bases does a rational produce a period, in which not?

Plenty of wondrous questions left to explore! And that is still in the rationals alone. Now, after we have made the jump to real numbers, all kinds of other questions pop up beyond the mere existence of irrationals. These questions touch on what should "count" as a number (pardon the pun) in a deep and even philosophical way, and not without controversy. This is a worthwhile, but nevertheless very accessible topic for students with lots of occasions for reflection and discussion, without reliance on abstract notation. And a topic for another time.

Part 3: Getting to the root

An Irrational Irrationality Proof

Remember this lesson from math class?

Theorem. The square root of 2 is an irrational number, i. e. it cannot be expressed as the ratio $\frac{p}{q}$ of two integers $p$ and $q$.

Proof. Suppose the contrary: that it is possible to write $\sqrt 2 = \frac pq$ for some (positive) integers $p$ and $q$. Suppose also that $\frac{p}{q}$ is already the reduced representation, so that $p$ and $q$ have no common divisors.
Then we can square both sides: $\left(\frac pq\right)^2 = \frac{p^2}{q^2} = 2$ and multiply by $q^2$: $p^2 = 2q^2$. So $p^2$ is the double of a natural number ($q^2$), and therefore even. But this can only be if $p$ itself is even. Thus $p$ can be written as $2k$, for some natural number $k$. Inserting this back yields: $(2k)^2 = 2q^2$ $\Rightarrow 4k^2 = 2q^2$ $\Rightarrow 2k^2 = q^2.$ Now we see that $q^2$ as well is even (twice the natural number $k^2$). So $q$ can also only be even.
But this means that $\frac pq$ can be reduced, since both $p$ and $q$ have the common divisor 2! This contradicts our assumption. Therefore $\sqrt 2$ cannot be a rational number.

□

This means that the set of rational numbers $\mathbb Q$ does not fill the number line, and needs to be expanded into the set of real numbers $\mathbb R$.

Even if you don't remember that particular lesson, I can assure that you have sat through it. This proof is an immovable pillar of any middle or high school curriculum. It appears almost to the letter in every textbook, and transcends cultures and ages. It can be traced back, minus the modern notation, to the Pythagoreans of Ancient Greece. (Cue the drowning myth.)

Problems with the Proof

The proof is lacking, not in correctness, but in its place in math class.

• It uses algebra to prove a result of arithmetic: namely, the existence of irrational numbers. Very often, the lessons that follow contain very little algebra, but focus on the number line, number sets, set notation etc. So why would we need algebra in the first place? Algebra is fine and important, but we teachers should recognize when it is not only unnecessary, but actively obfuscating. This is the case here.
• It uses algebra in an unusual way: the starting point is an equation, but containing two variables, and the equation is still unsolved by the end. Rather, the first line is the one that looks closest to a solved form, and a third variable is introduced. The nonproficient student is easily baffled by this moonwalking calculation and onslaught of letters. The variables are hard to tell apart, as the various expressions resemble each other a lot. Only by the end, and to whoever is still following, does it become clear that $p$, $q$ and $k$ are strawmen and have no actual values.
• The result is very narrow: naturally, one might ask about $\sqrt 3$, $\sqrt 5$, etc. Sometimes their irrationality is given as an exercise. But already for $\sqrt 6$, and in general the square root of composite numbers, the proof scheme breaks down. Students are told, or can guess from their calculators, that "most" square roots of the naturals (and rationals) are, indeed, irrational. But why not prove this, too? It can be done, with zero extra effort, using the right approach.
• The proof also demonstrates more than necessary: if the goal is merely to show that irrational numbers exist, there are easier examples, closer to what they look like in practice, such as Champernowne's constant 0.12345678910111213141516... (Of course, this presupposes the knowledge that a rational's decimal representation is either terminating or repeating. A valuable result which can also be demonstrated purely arithmetically.)

There is a better way

All in all, while the proof is a nifty piece of mathematics in a curriculum that is sorely lacking when it comes to proofs and abstract reasoning, we can do better.

The crux of the problem, in my view, is the mingling of two topics (irrationals and square roots) that are better treated separately. One can reason about rational and irrational numbers without even mentioning roots, and within arithmetic alone. This allows for a deeper appreciation of the fractional and decimal representation of numbers, their respective advantages and shortcomings, and the concept of number itself.

The fact that square roots are "usually" irrational can be investigated later, and in a manner that gives a simple and precise condition on the radicand while making no unnecessary use of algebra.

Over the next few posts, I will expand on this alternative approach. Stay tuned!

Part 2: The wondrous and mysterious rational numbers

Part 3: Getting to the root

I've got 99 Word Problems (part II)

This is part II of a two-part piece on a novel approach to solving word problems. Part I showed examples of using tables to solve a wide range of problems arithmetically. Now we look at situations without a direct solution, and that require us to set up an equation.

Are you feeling the power of the table yet?

Well then, let's keep riding that bronco as far as it will take us.

Step by step

A staircase is 40 steps high. If each step were 2.4 cm higher, then 5 steps could be saved while retaining the same overall height. How tall is the staircase?

The table for this problem looks innocent enough, but something is a little off:

After the first step, none of the remaining cells seem to be reachable! This is because they are arranged in a rectangular configuration. If any of them were known, we could easily complete the table, but as it stands, we seem to be at an impasse. What are we to do?

This:

And just like that, we have found an equation in the unknown original step height x (in cm): it is 40x = 35(x + 2.4), readily solved to yield x = 16.8 cm. The total height is then determined by either 40x or 35(x + 2.4) = 672 cm.

Why are equations so hard to find?

In my experience, students' difficulties with setting up an equation stem in no small part from an inexperience with setting up expressions. This is an essential prerequisite an usually neglected beforehand. Working with expressions often is restricted to algebraic manipulations of given expressions. The skill of coming up with your own expressions to model a problem is mostly trained within other mathematical contexts, e. g. linear functions or word problems. In both contexts, finding an appropriate expression is merely the first part of a problem, while the focus is set on what follows.

No wonder students get frustrated when the list of steps and skills required for the solution is so long. Jumping from the formal manipulations of algebra right into word problems that require an equation is a steep increase in complexity. In his seminal book How to Solve It, G. Pólya recommended guiding questions for the student struggling with finding an equation:

• What is the unknown? What are the data? What is the condition?
• Keep only a part of the condition, drop the other part: how far is the unknown then determined, how can it vary?
• Could you derive something useful from the data?
• Could you think of other data suitable to determine the unknown?
• Could you change the unknown or the data, or both if necessary, so that the new unknown and the new data are nearer to each other?

The problem with these questions is their abstract language: "data", "condition", "determined" – these are terms that are only understood by someone who already grasps the conceptual framework of expressions and equations. They are part of a meta-language, useful for educators to talk to each other, but possibly impenetrable to the novice. Understanding them is the ultimate goal here, and cannot be the starting point.

Enough musings on the general – let's see the table method in action in a few more problems!

Cold, hard cash

This next one is a favorite among teachers, at least here in Switzerland. It concerns a situation any teenager can relate to:

A capital of 920 000 € is being invested in two parts: the first investment yields 1.25 % annually, the second has an annual profit of 2.75 %. After one year, the capital has grown to 940 200 €. How has the initial amount been split?

The table looks familiar:

And again, the unknown quantities are arranged in a rectangular fashion. We set an unknown x for the first investment and complete:

The equation can be read off in the right column:

0.0125 x + 0.0275(920 000 – x) = 20200    ⇒    x = 340 000 €.
Hence the first investment was 340 000 € and the second 580 000 €.

The Last Airbender

One final example:

What determines whether a body submerged in water will float or sink? It is the ratio between its mass and its volume, i. e. its average density. If it is greather than the density of water (1 kg/dm³), the body will sink, otherwise buoyancy will keep it afloat. The human body has an average density of 1.062 kg/dm³, but this can be lowered by inhaling air (density: 1.2 g/dm³). How much air does a person weighing 65 kg have to inhale to play "dead man"?

Here we go:

We get the equation 61.2x = 65 + 0.0012x for the volume of air x, and therefore x ≈ 3.8 dm³.

Closing remarks

Tables are but one, though powerful, way of representing mathematical relationships. They can be used to great benefit in many other parts of the school curriculum, but can only supplement other representations (graphs, drawings etc.). As much as they formalize common aspects of word problems, they cannot replace actual understanding at the semantic level. Still I deem them a fruitful method to give structure to a topic feared by many for its seemingly arbitrary solution methods.

Addendum: A few more problems for the road

1. Already a single glass of orange juice (250 ml) covers an adult's daily recommended dose of vitamin C. Grapefruit juice contains 44 mg/l less vitamin C, whoever wants to cover their daily dose with it should pour themselves a slightly larger glass (280 ml). How much vitamin C does an adult need per day?

2. The French high-speed train TGV travels the track from Paris to London (total length 495 km) in three sections:

• Paris-Calais in 80 min
• Calais-Ashford (the Chunnel) in 24 min
• Ashford-London in 30 min

Between Paris and Calais, the TGV travels 70 km/h faster than on the rest of the track. How fast is that, and how long are the three sections?

3. At a charity run over 25 km, an inexperienced runner leaps ahead of everyone else, until he is short of breath after 5 km. After that, he can only run at half his initial speed. He keeps his pace for the remainder of the race and reaches the finish line after 90 min. How fast was he running at the beginning?

4. Carl is again mixing coke with orange juice. How much orange juice (sugar concentration 70 g/l) must he mix with 200 ml of coke (sugar concentration 106 g/l), so that the mix contains 80 g/l of sugar?

5. A cocktail is composed of 4 cl of vodka (40% alcohol), 10 cl of orange juice and a dash of amaretto (28% alcohol). How large must the dash be so that the total alcohol content does not exceed 12%?

I've got 99 Word Problems (part I)

The Table Method: How to approach high school word problems in a unified and systematic way

It was a math lesson like countless before. It was early March, and the entrance exam for the prestigious Swiss upper high schools was approaching fast. I had been preparing my students, 'in-betweeners' who had not passed the first time, extensively. Ten math lessons per week, non-stop exam preparation, since August. We had covered the whole curriculum and were reviewing selected topics.

This particular day was dedicated to word problems. We were discussing a standard, run-of-the-mill time-distance problem:

A cyclist takes 15 min to complete the first leg of a trip, if she cycles at a speed of 24 km/h. Find out how fast she has to travel on the second leg, measuring 10 km, so that her average speed over the whole distance is 22.5 km/h.

There are more exciting problems to wonder about in mathematics, but that is a topic (read: rant) for another day. In class, we went through the usual steps:

1. the first leg ist 0.25 h x 24 km/h = 6 km long
2. the total distance is therefore 6 km + 10 km = 16 km
3. the total travel time is 16 km / 22.5 km/h = 0.71 h ( = 42 min 40 s)
4. the travel time on the second leg is therefore 0.71 h – 0.25 h = 0.461 h ( = 27 min 40 s)
5. the speed over the the second leg is thus 10 km / 0.461 h ≈ 21.7 km/h

Did I say we went through these steps? My bad, I meant I. My students could follow each one of them, but were at a complete loss on how to find them in the first place. It seemed like black magic, but then again: "Mr. Hambrecht, when you explain it, it's obvious!"

How often had I been with a class at that exact same spot? I've lost count.

WHY ARE WORD PROBLEMS SO HARD?

One of the main difficulties with word problems is the inability to recognize where to start. The above problem contains four given quantities, and requires five steps to solve. This is far beyond the one- or two-step problems from elementary school. Students can feel overwhelmed by the sheer number of possible combinations of given numbers and operations. Of course, most of those combinations make no sense, but that is exactly what separates the trained eye from the apprentice. How is a novice in chess supposed to choose from the 20 possible first moves? Or solve a chess problem? Even if they can follow other player's explanations on why a particular move is good, and another bad, they will often be hard-pressed to come up with their own.

I bring up this analogy because word problems, much like chess, lack a unifying system for finding such solutions. Checking a given solution, on the other hand, is much easier. Patterns for finding good moves in chess exist, but they are so manifold that it still takes the proverbial 10 000 hours to learn them. When we try to teach pattern recognition in word problems, we encounter the same problem: the patterns are apparently so few and far between that each new problem effectively appears unique.

But this is not so. There exist deep, unifying and beautiful analogies between the plethora of seemingly unrelated word problems. They share common algebraic structures whose representations can please the aesthetic sensibility in any mathematician's mind. The following examples will show what I mean.

CYCLING BACK

Let's go back to that fateful math lesson. We were all looking puzzled at the worked solution on the blackboard. The students wondering how to get to such a solution on their own, me wondering how to get that skill from my head into theirs.

But then something happened. Out of the blue, perhaps just to summarize, I drew a table:

There are three triplets of the relationship "time x speed = distance", one for each leg and one for the whole trip: those are the rows. And of course, the times and distances add up (but not the speeds): those are the columns. With these links in mind, the steps for completing the table fell into place (click on the arrows to show them):

"It's just like a sudoku!" exclaimed one of the students.

For the first time, a time-distance problem seemed tractable to them. Graphing the problem helps to visualize it, but gives no immediate clues on how to actually compute an answer. In a table, the known and unknown quantities are ordered along their algebraic relationships, immediately suggesting each next step.

We all learned something that day. I made a mental note of exploring this method for other kinds of problems. Over the following days and lessons, it dawned on me just how powerful it was.

GIMME SUGAR

The word problems in the entrance exams seemed to be tailored for precisely this method: a lot of them e. g. invariably contained some sort of weighted average, without calling it such. Here is another example:

Carl likes to mix coke with orange juice, to make it less sweet. Coke has a sugar concentration of 106 g/l, while orange juice contains 70 g of sugar per liter. Now Carl is mixing 50 ml of orange juice with a threefold quantity of coke. What is the sugar concentration (in g/l) of the mix?

Three columns, linked by multiplication:

volume (l) x sugar concentration (g/l) = sugar content (g).

Three rows: pure coke, pure orange juice, and the mix. Again, volumes and sugar contents add up, but not the concentrations:

The red arrow represents the datum "three times more coke than orange juice". We get to the concentration by first finding everything else:

The algebraic structure of this problem is exactly the same as in the previous time-distance problem. Instead of an average speed, we have an average concentration (which becomes realized once the coke and juice mix). Only the distribution of known and unknown quantities has changed. 

CECI N'EST PAS UNE PIPE

But the really funny thing is that tables can also be used to solve other, apparently unrelated kinds of word problems:

The incoming pipe of a sewage treatment plant can fill the sewage bassin (volume 2000 m³) in 50 min. A second pipe is being built, capable of carrying twice as much water per minute. How long will it take both pipes at once to fill the bassin?

Once more we are dealing with three quantities related by multiplication:

time (min) x discharge (m³/min) = volume (m³).

And once again, they occur in three variants: once for each pipe and once for both of them together. But there is a crucial difference to the previous problems: it is now the "rate", or "density", quantity that is additive, and none of the other two. In fact, the volume is the same in all three rows, since we compare three possible ways of performing the exact same task.

Keeping these changed relationships in mind, we can complete the table:

In fact, the bassin's volume is irrelevant, as one can check by algebra or common sense. This brings us to one of teachers's favourite problems.

WORK IT HARDER, MAKE IT BETTER

You knew this one would come.

Annie takes 5 h to complete a certain task, Bertie needs 8 h for the same work. How long will they take working together?

Of course, this depends on the kind of task at hand. But we are in math class here and thus there are no other kinds of work than the continuously divisible kind, such as digging holes and painting fences. The formulation of the problem is abstract enough that many students do not realize the wrongness of simply adding (or subtracting) the durations. In a tabular setup, and with the preparation of volume-filling problems, it becomes much clearer which quantities can be added and which ones cannot. Also, the need for an arbitrary number for the total workload can be addressed more clearly when faced with a table that is too sparse to complete, but otherwise analogous to the previous problem:

All these problems could be solved purely arithmetically. In part II, we will see how the table method extends to problems requiring an equation in an unknown. It is astonishing how many textbook word problems fit one of these basic tables, or simple variations of them – so stay tuned!

ADDENDUM

Here are a few more word problems that can be solved with the table method.

1. A group of people is taking the train. The tickets costs 84 € per person, unless they have a half-fare card. The total price for the trip is 3990 €. If 15 people of the group carry a half-fare card, how many are in the group?

2. A volume of 50 g of concentrated hydrochloric acid (HCl, 90 % concentration) is being mixed with 200 g of more diluted HCl (15 % concentration). As the resulting solution is still too strong, it is being diluted with water. How much water does one have to add to achieve a concentration of 5 %?

3. A stadium is being fitted with 5500 additional seats and a second exit. The old exit could empty the whole stadium (22 000 sports fans) in 44 min. The new, wider exit can empty the new stadium by itself in half the time. How long will it take to evacuate using both exits together?

4. A swimming pool can be filled in 45 min and drained in 50 min. How long will it take to fill if the janitor forgets to close the drain?