This is part II of a two-part piece on a novel approach to solving word problems. Part I showed examples of using tables to solve a wide range of problems arithmetically. Now we look at situations without a direct solution, and that require us to set up an equation.
Are you feeling the power of the table yet?
Well then, let's keep riding that bronco as far as it will take us.
Step by step
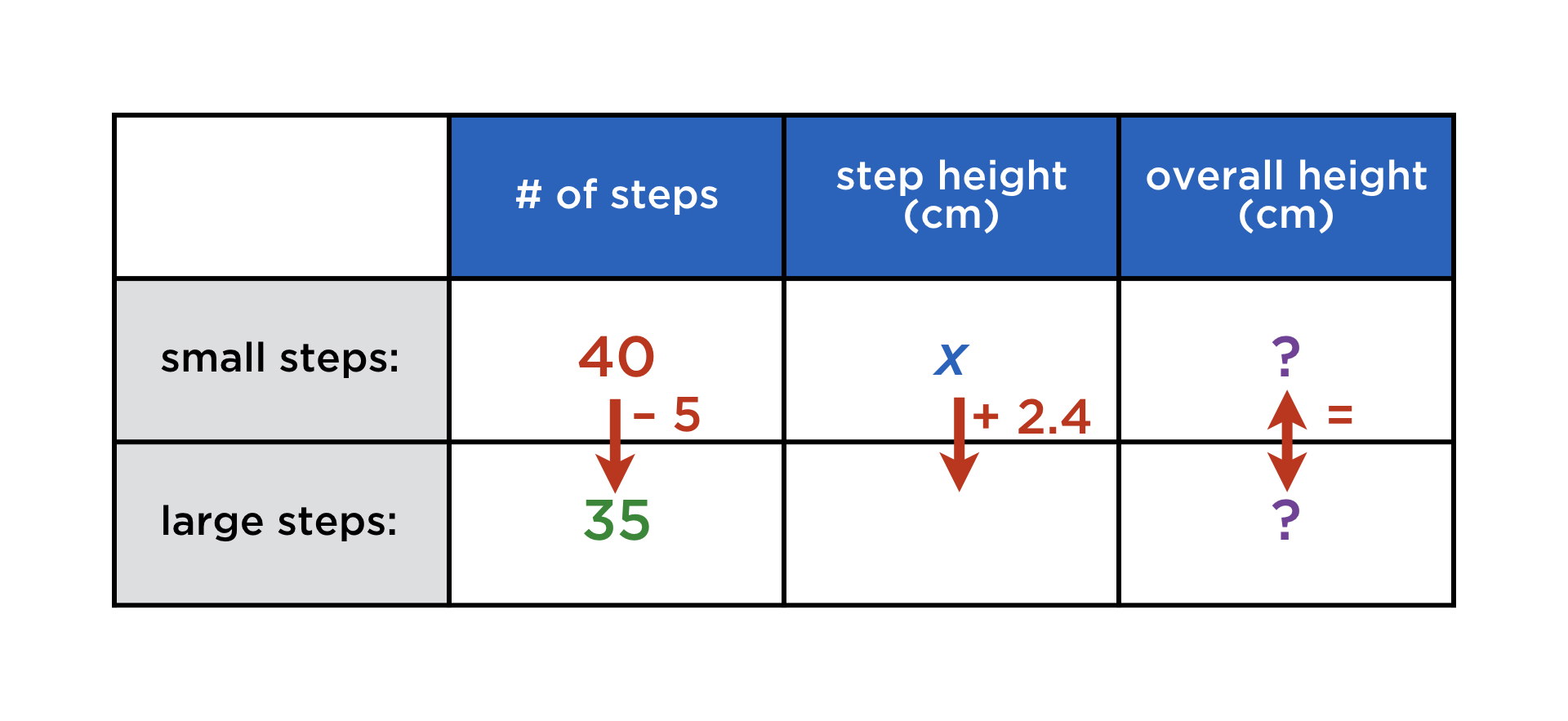
A staircase is 40 steps high. If each step were 2.4 cm higher, then 5 steps could be saved while retaining the same overall height. How tall is the staircase?
The table for this problem looks innocent enough, but something is a little off:
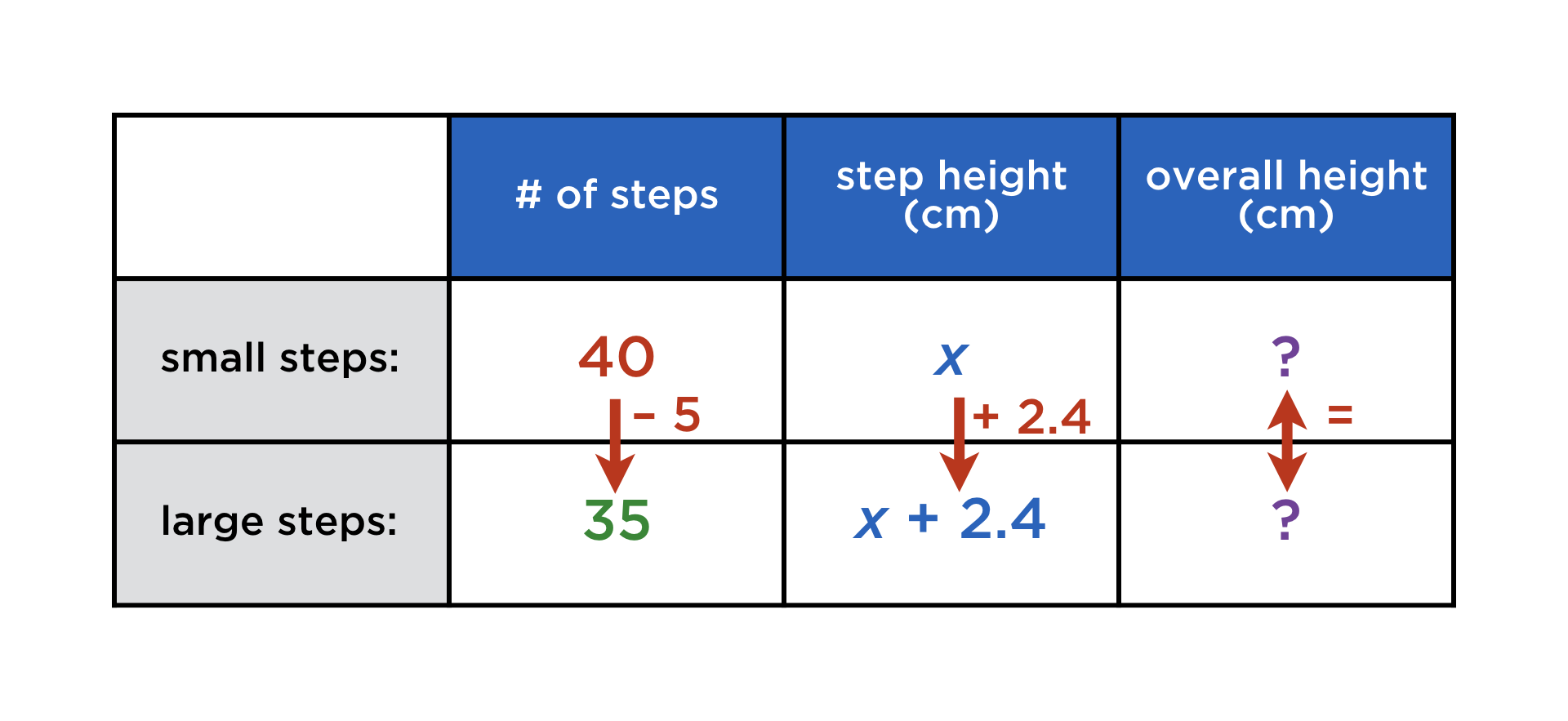
After the first step, none of the remaining cells seem to be reachable! This is because they are arranged in a rectangular configuration. If any of them were known, we could easily complete the table, but as it stands, we seem to be at an impasse. What are we to do?
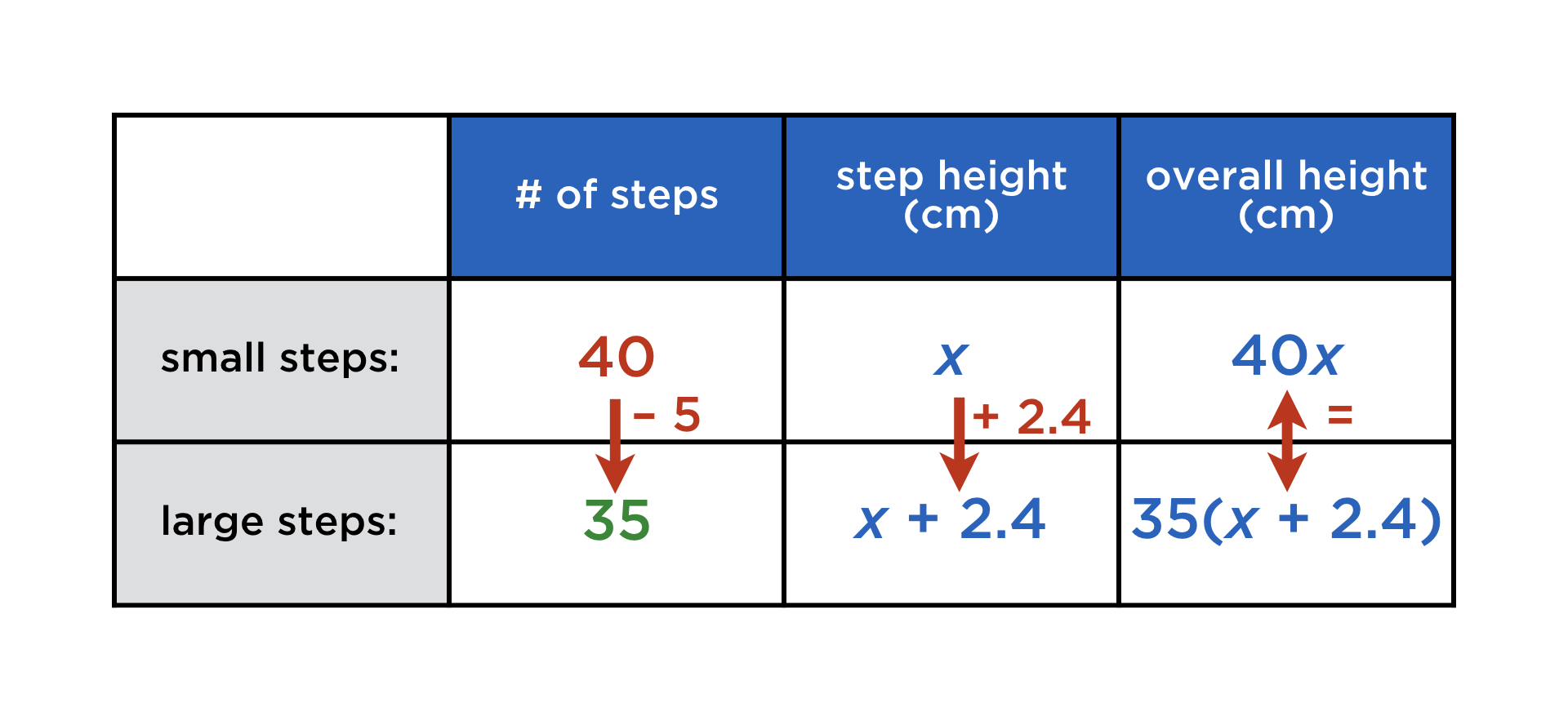
This:
And just like that, we have found an equation in the unknown original step height x (in cm): it is 40x = 35(x + 2.4), readily solved to yield x = 16.8 cm. The total height is then determined by either 40x or 35(x + 2.4) = 672 cm.
Why are equations so hard to find?
In my experience, students' difficulties with setting up an equation stem in no small part from an inexperience with setting up expressions. This is an essential prerequisite an usually neglected beforehand. Working with expressions often is restricted to algebraic manipulations of given expressions. The skill of coming up with your own expressions to model a problem is mostly trained within other mathematical contexts, e. g. linear functions or word problems. In both contexts, finding an appropriate expression is merely the first part of a problem, while the focus is set on what follows.
No wonder students get frustrated when the list of steps and skills required for the solution is so long. Jumping from the formal manipulations of algebra right into word problems that require an equation is a steep increase in complexity. In his seminal book How to Solve It, G. Pólya recommended guiding questions for the student struggling with finding an equation:
- What is the unknown? What are the data? What is the condition?
- Keep only a part of the condition, drop the other part: how far is the unknown then determined, how can it vary?
- Could you derive something useful from the data?
- Could you think of other data suitable to determine the unknown?
- Could you change the unknown or the data, or both if necessary, so that the new unknown and the new data are nearer to each other?
The problem with these questions is their abstract language: "data", "condition", "determined" – these are terms that are only understood by someone who already grasps the conceptual framework of expressions and equations. They are part of a meta-language, useful for educators to talk to each other, but possibly impenetrable to the novice. Understanding them is the ultimate goal here, and cannot be the starting point.
Enough musings on the general – let's see the table method in action in a few more problems!
Cold, hard cash
This next one is a favorite among teachers, at least here in Switzerland. It concerns a situation any teenager can relate to:
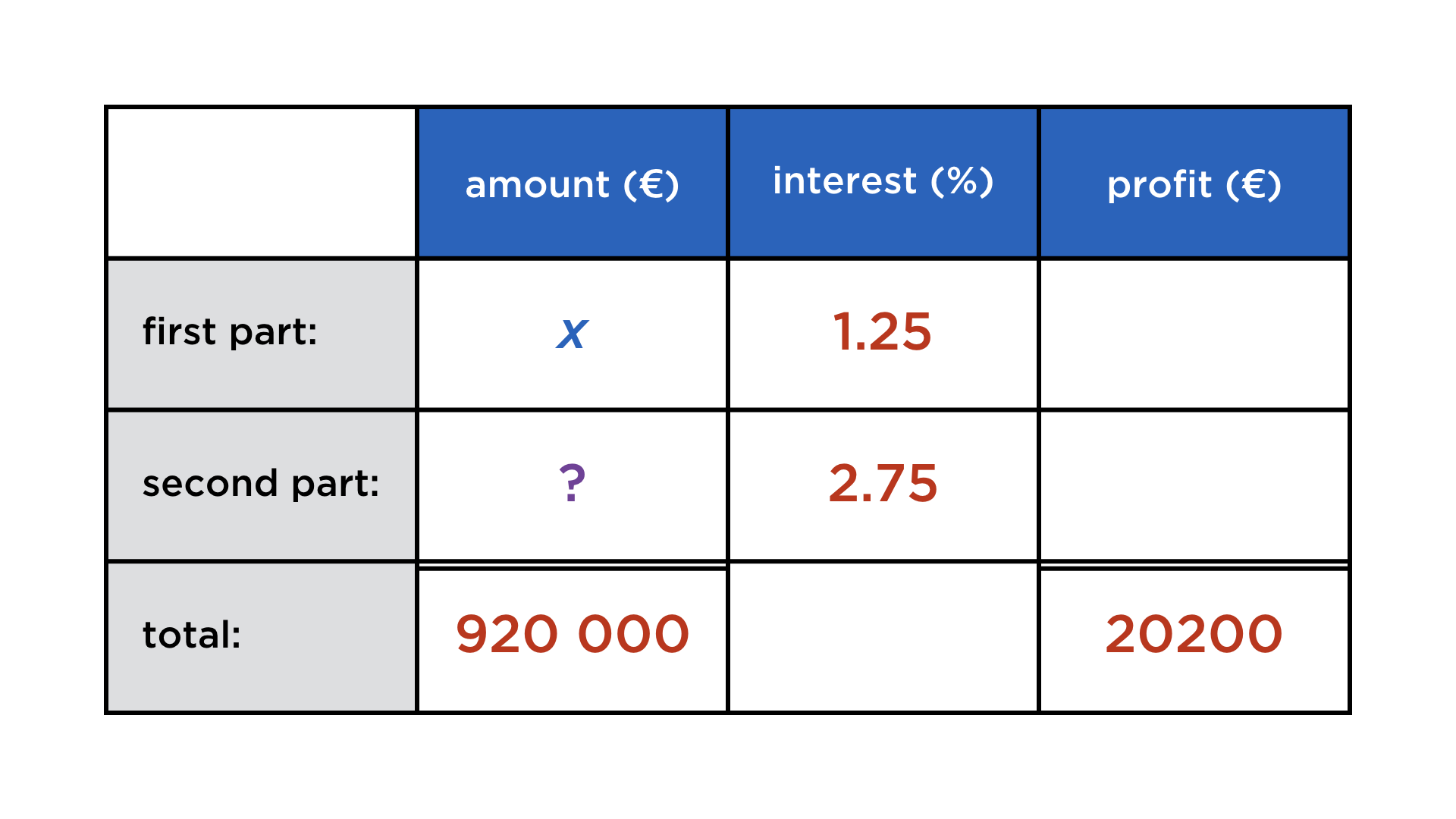
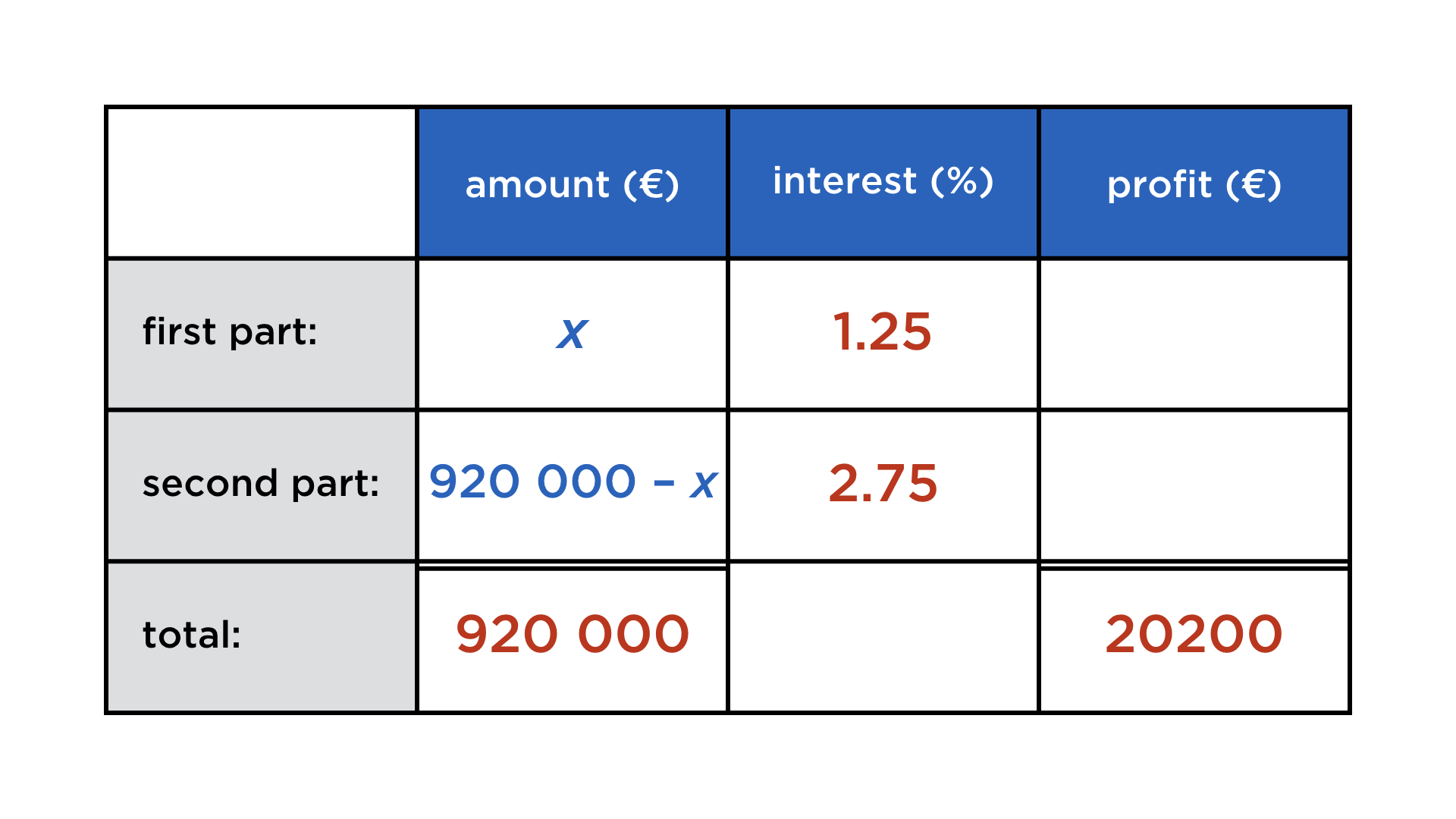
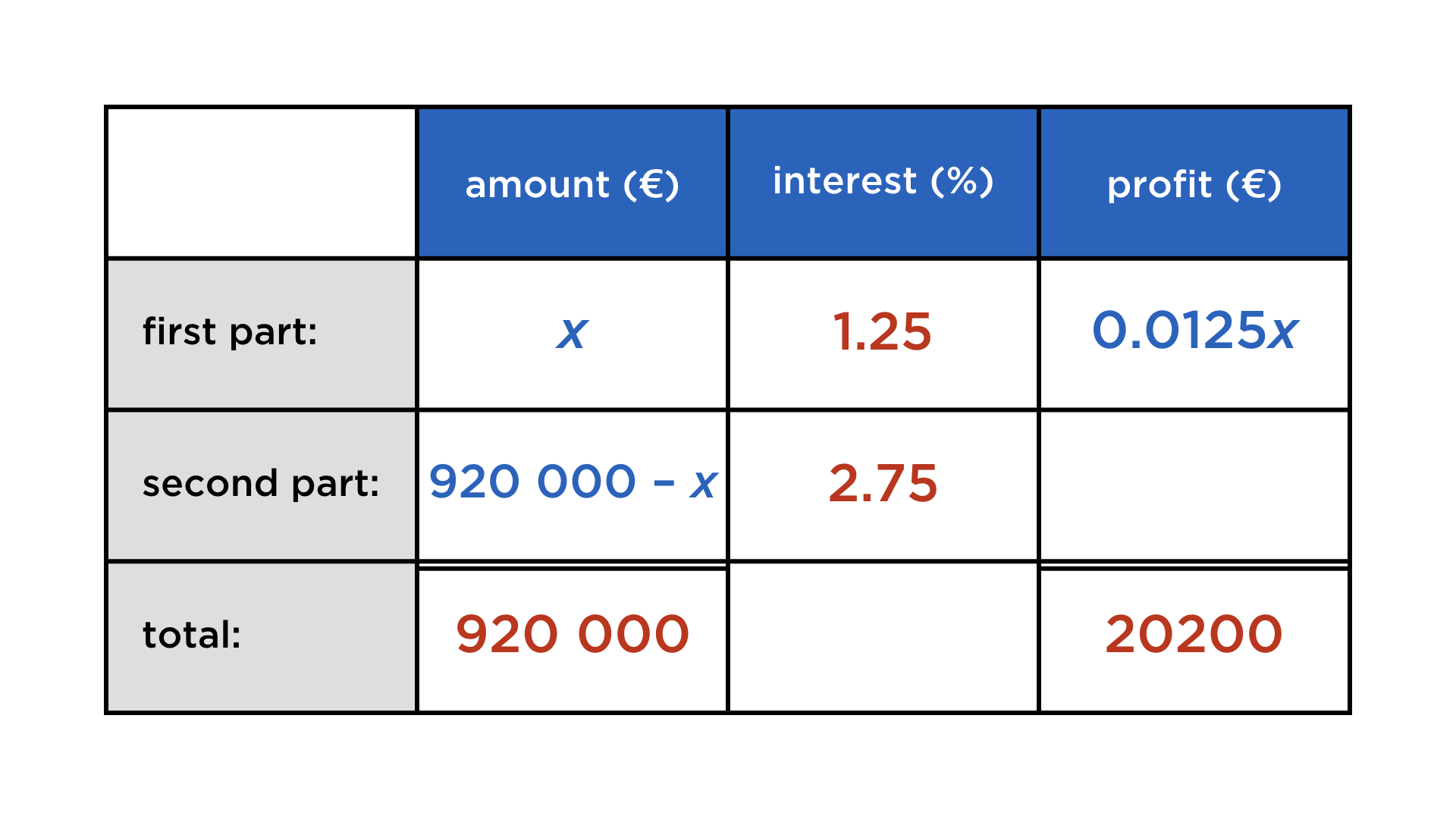
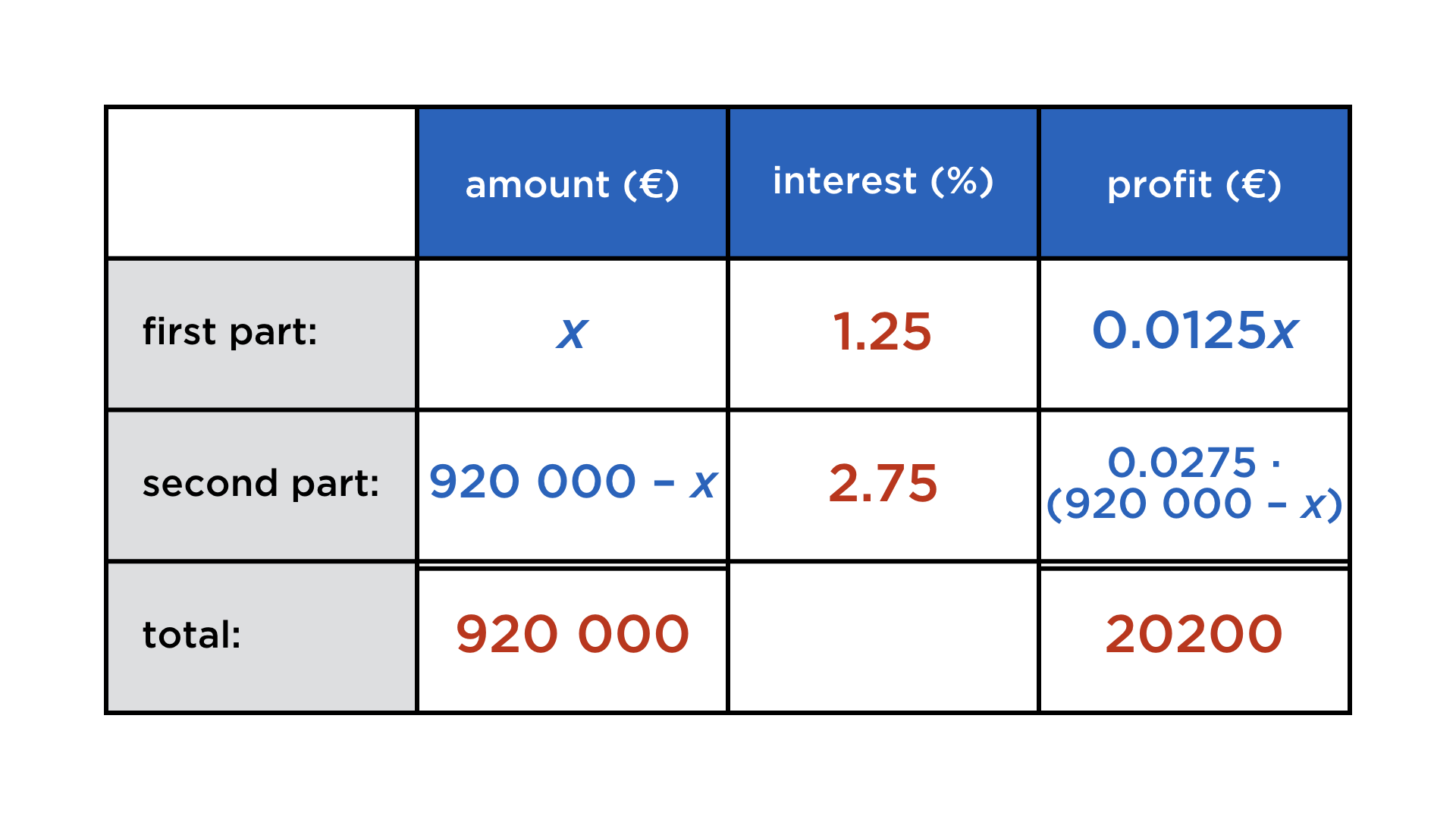
A capital of 920 000 € is being invested in two parts: the first investment yields 1.25 % annually, the second has an annual profit of 2.75 %. After one year, the capital has grown to 940 200 €. How has the initial amount been split?
The table looks familiar:
And again, the unknown quantities are arranged in a rectangular fashion. We set an unknown x for the first investment and complete:
The equation can be read off in the right column:
Hence the first investment was 340 000 € and the second 580 000 €.
The Last Airbender
One final example:
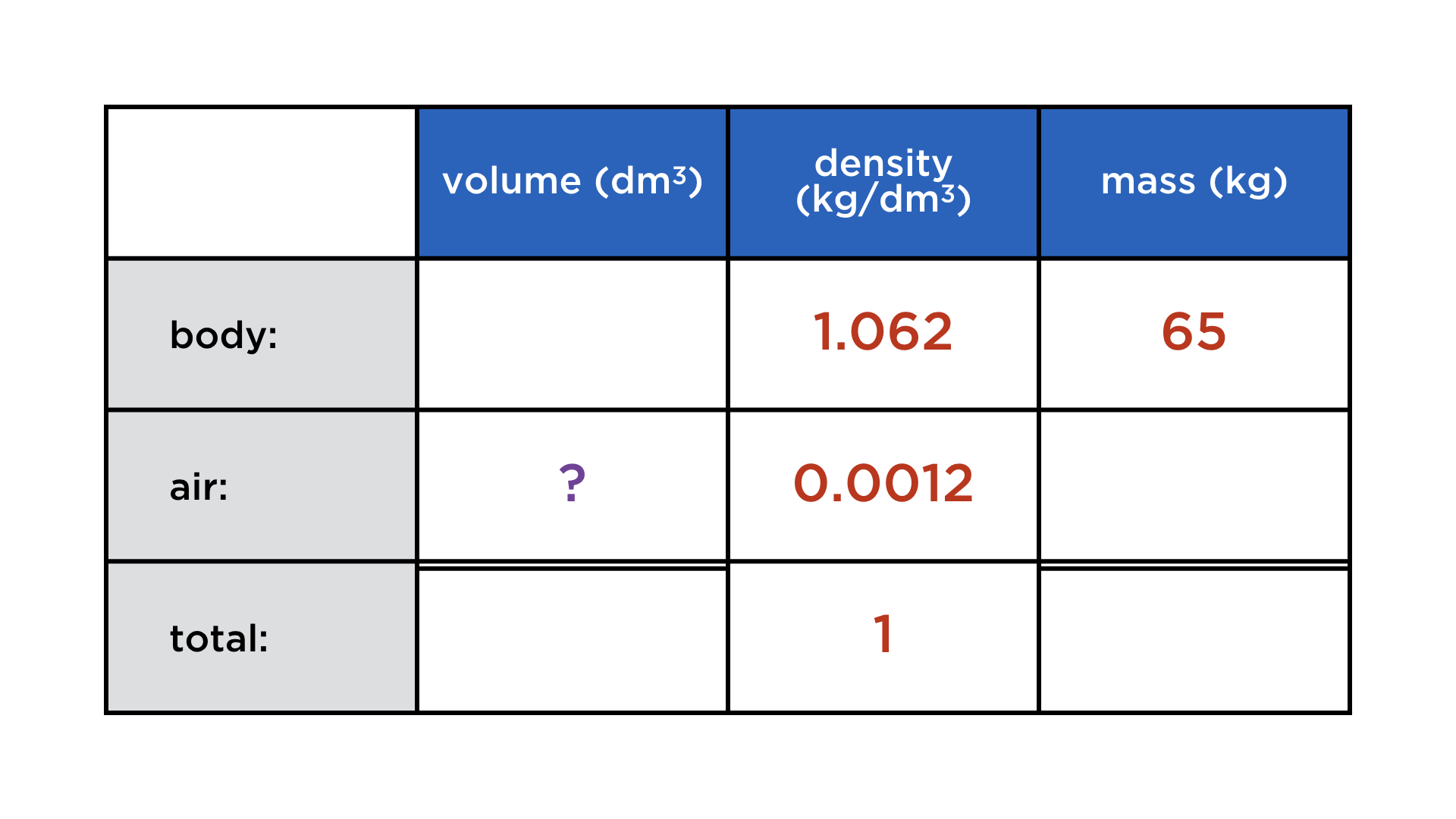
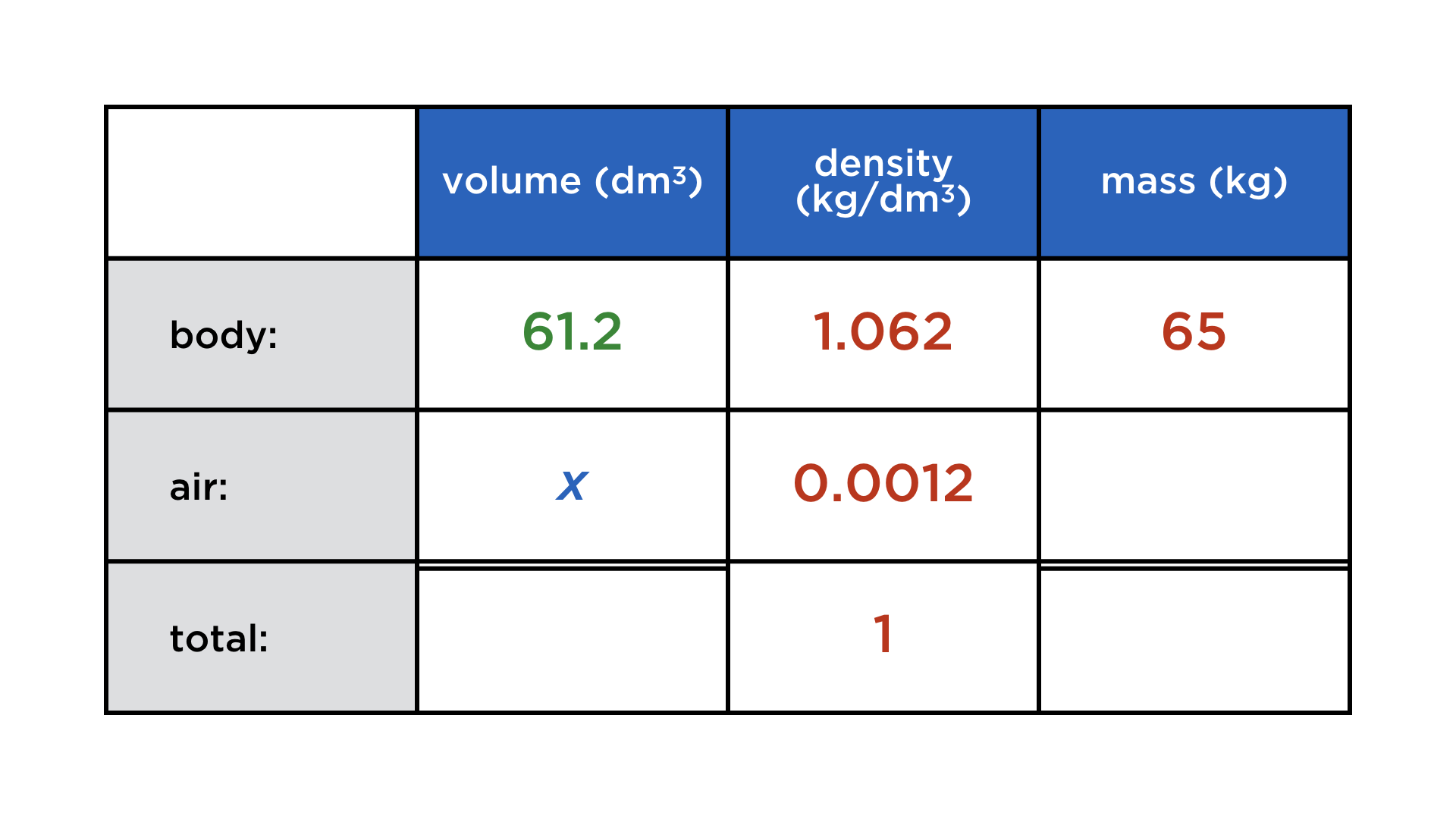
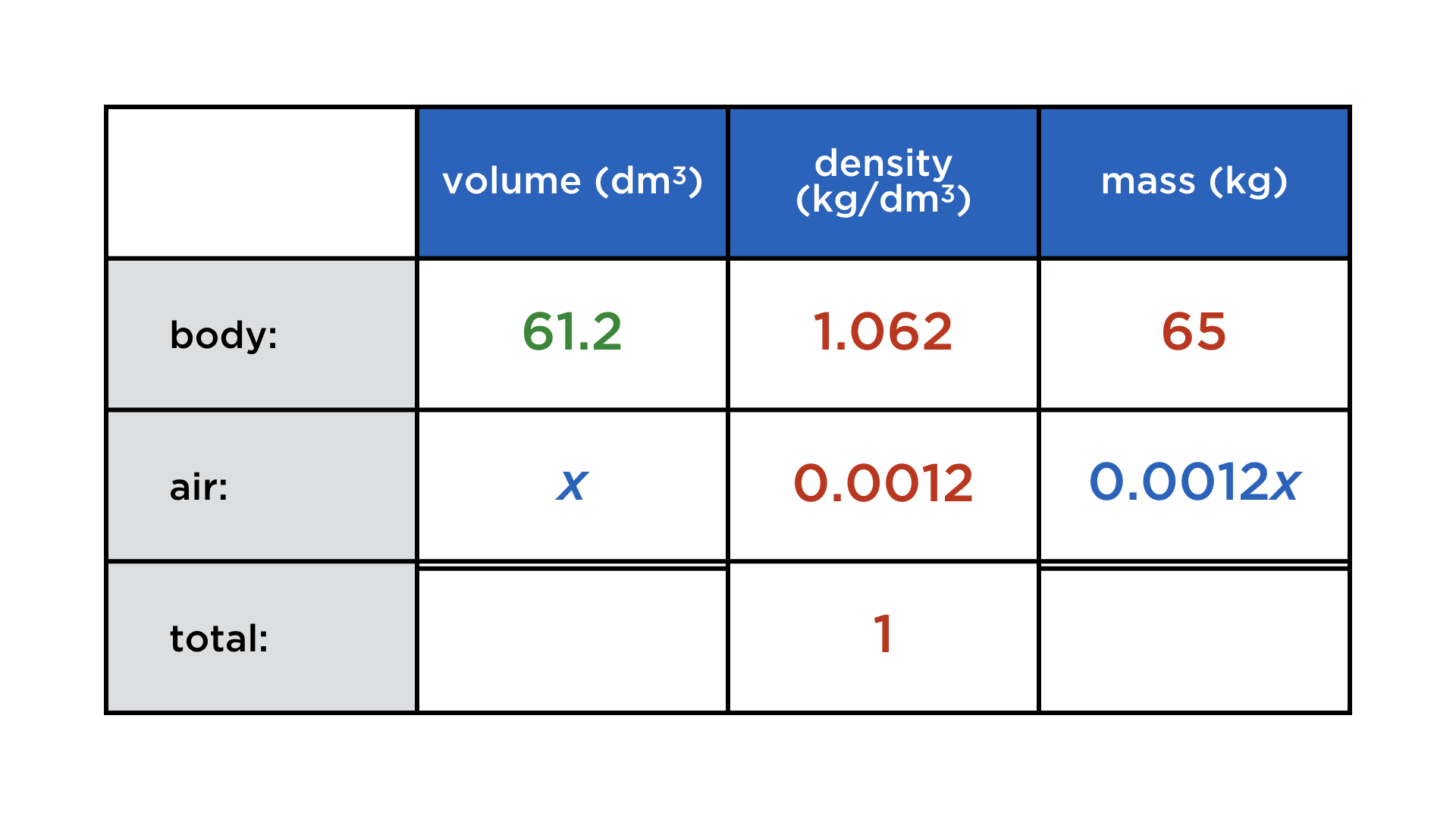
What determines whether a body submerged in water will float or sink? It is the ratio between its mass and its volume, i. e. its average density. If it is greather than the density of water (1 kg/dm3), the body will sink, otherwise buoyancy will keep it afloat. The human body has an average density of 1.062 kg/dm3, but this can be lowered by inhaling air (density: 1.2 g/dm3). How much air does a person weighing 65 kg have to inhale to play "dead man"?
Here we go:
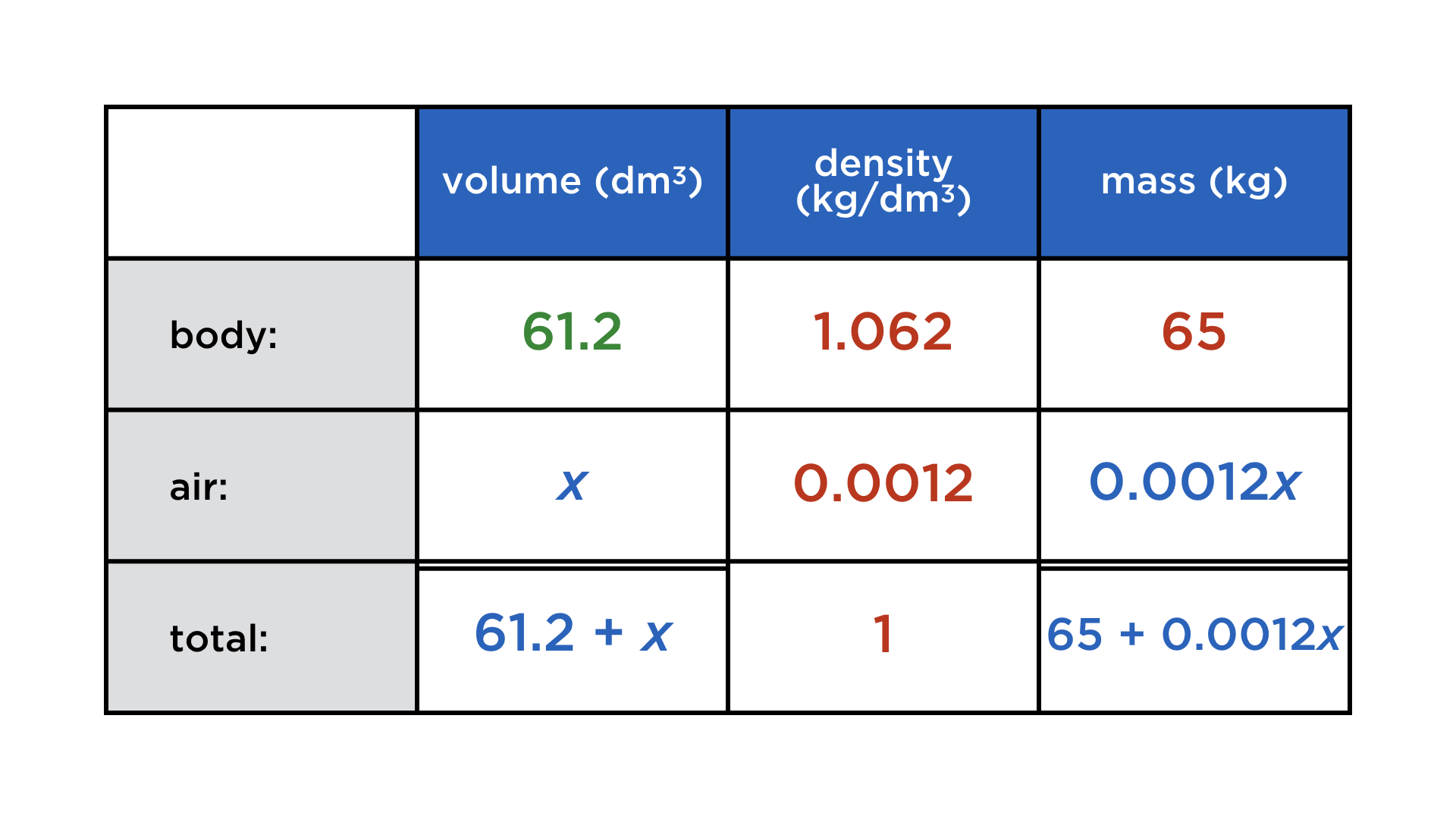
We get the equation 61.2x = 65 + 0.0012x for the volume of air x, and therefore x ≈ 3.8 dm3.
Closing remarks
Tables are but one, though powerful, way of representing mathematical relationships. They can be used to great benefit in many other parts of the school curriculum, but can only supplement other representations (graphs, drawings etc.). As much as they formalize common aspects of word problems, they cannot replace actual understanding at the semantic level. Still I deem them a fruitful method to give structure to a topic feared by many for its seemingly arbitrary solution methods.
Addendum: A few more problems for the road
1. Already a single glass of orange juice (250 ml) covers an adult's daily recommended dose of vitamin C. Grapefruit juice contains 44 mg/l less vitamin C, whoever wants to cover their daily dose with it should pour themselves a slightly larger glass (280 ml). How much vitamin C does an adult need per day?
2. The French high-speed train TGV travels the track from Paris to London (total length 495 km) in three sections:
Between Paris and Calais, the TGV travels 70 km/h faster than on the rest of the track. How fast is that, and how long are the three sections?
3. At a charity run over 25 km, an inexperienced runner leaps ahead of everyone else, until he is short of breath after 5 km. After that, he can only run at half his initial speed. He keeps his pace for the remainder of the race and reaches the finish line after 90 min. How fast was he running at the beginning?
4. Carl is again mixing coke with orange juice. How much orange juice (sugar concentration 70 g/l) must he mix with 200 ml of coke (sugar concentration 106 g/l), so that the mix contains 80 g/l of sugar?
5. A cocktail is composed of 4 cl of vodka (40% alcohol), 10 cl of orange juice and a dash of amaretto (28% alcohol). How large must the dash be so that the total alcohol content does not exceed 12%?